Question

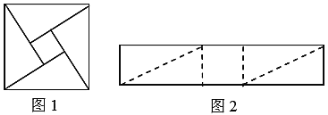
【题目】如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”．将图2的矩形分割成四个全等三角形和一个正方形，恰好能拼成这样一个“勾股圆方图”，则该矩形与拼成的正方形的周长之比为________．

Answer 1

【答案】（或）

【解析】

设图2的矩形分割成四个全等三角形的两直角边为a、b（a＞b），由图1与图2的两个小正方形相同，得出a与b的关系，再求出矩形的边长和大正方形的边长，应用周长公式求得其周长，最后便可求得其比值．

解：设图2的矩形分割成四个全等三角形的两直角边为a、b（a＞b），

则大正方形的边长为，

小正方形的边长为a-b，

矩形的长为2a+a-b=3a-b，宽为b，

∴矩形的周长为：2（3a-b+b）=6a，

由图2知，中间小正方形的边长为b，

∴a-b=b，

∴a=2b，

∴大正方形的周长为

∴该矩形与拼成的正方形的周长之比：

故答案为：3：（或 ：5）．