题目内容
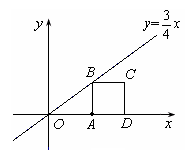
如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线 经过C、B两点,与x轴的另一交点为D。
经过C、B两点,与x轴的另一交点为D。

(1)点B的坐标为( , ),抛物线的表达式为 .
(2)如图2,求证:BD//AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长。
 经过C、B两点,与x轴的另一交点为D。
经过C、B两点,与x轴的另一交点为D。
(1)点B的坐标为( , ),抛物线的表达式为 .
(2)如图2,求证:BD//AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长。
(1)(6,2) (2)见解析(3)8
(2)见解析(3)8
 (2)见解析(3)8
(2)见解析(3)8解:(1)(6,2); 。
。
(2)证明:令 ,即
,即 ,解得x=2或x=7。
,解得x=2或x=7。
∴D(7,0)。
∴BC=AC= ,BD=
,BD= ,CD=5。∴
,CD=5。∴ 。
。
∴∠CBD=900,即BD⊥BC。
又∵ AC⊥BC,∴BD//AC。

(3)连接AB,BP,
∵AC⊥BC,BC=AC= ,
,
∴∠ACB=900,∠ABC=450,∠APB= ∠ACB=450,AB=
∠ACB=450,AB= 。
。
∴∠ABQ=∠APB。
又∵∠BAQ=∠PAB,∴△ABQ∽△APB。
∴ ,即
,即 ,解得AP=8。
,解得AP=8。

(1)过点B作BE⊥x轴于点E,易证△AOC≌△CEB(AAS),则
CE=AO=4, BE=CO=2,OE=6,∴B(6,2)。
将B(6,2),C(2,0)代入 ,得
,得
 ,解得
,解得 。
。
∴抛物线的表达式为 。
。
(2)应用勾股定理求出BC,BD和CD的长,根据勾股定理逆定理得∠CBD=900,即BD⊥BC,从而由AC⊥BC,得到BD//AC。
(3)连接AB,BP,通过证明△ABQ∽△APB得 求解。
求解。
别解:
①过点C作CH⊥AQ于点H,由垂径定理和射影定理求解。
②由勾股定理求得 延长BC交⊙O于点R,由相交弦定理求解。
延长BC交⊙O于点R,由相交弦定理求解。
 。
。(2)证明:令
 ,即
,即 ,解得x=2或x=7。
,解得x=2或x=7。∴D(7,0)。
∴BC=AC=
 ,BD=
,BD= ,CD=5。∴
,CD=5。∴ 。
。∴∠CBD=900,即BD⊥BC。
又∵ AC⊥BC,∴BD//AC。

(3)连接AB,BP,
∵AC⊥BC,BC=AC=
 ,
,∴∠ACB=900,∠ABC=450,∠APB=
 ∠ACB=450,AB=
∠ACB=450,AB= 。
。∴∠ABQ=∠APB。
又∵∠BAQ=∠PAB,∴△ABQ∽△APB。
∴
 ,即
,即 ,解得AP=8。
,解得AP=8。
(1)过点B作BE⊥x轴于点E,易证△AOC≌△CEB(AAS),则
CE=AO=4, BE=CO=2,OE=6,∴B(6,2)。
将B(6,2),C(2,0)代入
 ,得
,得 ,解得
,解得 。
。∴抛物线的表达式为
 。
。(2)应用勾股定理求出BC,BD和CD的长,根据勾股定理逆定理得∠CBD=900,即BD⊥BC,从而由AC⊥BC,得到BD//AC。
(3)连接AB,BP,通过证明△ABQ∽△APB得
 求解。
求解。别解:
①过点C作CH⊥AQ于点H,由垂径定理和射影定理求解。
②由勾股定理求得
 延长BC交⊙O于点R,由相交弦定理求解。
延长BC交⊙O于点R,由相交弦定理求解。
练习册系列答案
相关题目

 )
) 与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
 ,求N点坐标;
,求N点坐标;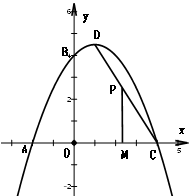
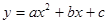 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与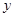 轴交于负半轴.给出四个结论:①abc<0;②2a+
轴交于负半轴.给出四个结论:①abc<0;②2a+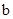 >0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .
>0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .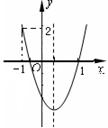
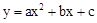 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
 与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )
与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )
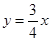 ,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线
,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线