题目内容
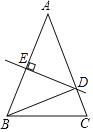
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长;
(2)若∠CBD=30°,试求△ABC三个角的度数.
【答案】(1)BE=6cm;(2)∠A=40°,∠ABC=70°,∠C=70°.
【解析】
(1)根据线段垂直平分线的性质得到AD=DB,AE=BE,根据三角形的周长公式求出AB,即可得出结论;
(2)根据等腰三角形的性质得到∠A=∠ABD=α,根据等腰三角形的性质、三角形内角和定理计算即可.
(1)∵DE是边AB的垂直平分线,
∴AD=DB,AE=BE.
∵△BCD的周长为18cm,
∴AC+BC=AD+DC+BC=DB+DC+BC=AC+BC=18(cm).
∵△ABC的周长为30cm,
∴AB=30﹣(AC+BC)=30﹣18=12(cm),
∴BE=12÷2=6(cm);
(2)设∠A=α.
∵DA=DB,
∴∠A=∠ABD=α.
∵AB=AC,
∴∠C=∠ABC=α+30°,
由三角形的内角和定理得:α+2(α+30°)=180°,
解得:α=40°,
∴∠A=40°,∠ABC=70°,∠C=70°.

练习册系列答案
相关题目