题目内容
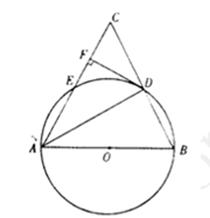
如图,⊙O是⊿ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则DE的长为( )


A. | B. | C. | D. |
D
试题分析:根据角平分线的性质及圆周角定理可得∠DBC=∠DAC=∠BAD,再结合公共角∠D即可证得△ABD∽△BED,根据相似三角形的性质即可求得结果.
∵AD平分∠BAC
∴∠DBC=∠DAC=∠BAD
∵∠D=∠D
∴△ABD∽△BED
∴

∵AD=5,BD=2
∴
 ,解得
,解得
故选D.
点评:解答本题的关键是熟记相似三角形的对应边成比例,注意对应字母写在对应位置上.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
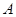 和圆
和圆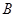 相切,两圆的圆心距为8cm,圆
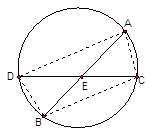
相切,两圆的圆心距为8cm,圆 , EF与GH是此外接圆的直径,EF=4,AD⊥GH,EF⊥GH,则图中阴影部分的面积是
, EF与GH是此外接圆的直径,EF=4,AD⊥GH,EF⊥GH,则图中阴影部分的面积是
 的圆形纸片折叠后,圆弧恰好经过圆心
的圆形纸片折叠后,圆弧恰好经过圆心 ,则折痕
,则折痕 的长为_____.
的长为_____.