题目内容
20.(1)解下列方程①x2+x-12=0
②3x2-6x+4=0
(2)已知关于x的一元二次方程(m-2)x2-4mx+2m-6=0有两个相等的实数根,求m的值.
分析 (1)①利用因式分解法,将x2+x-12=0变形为(x+4)(x-3)=0,解之即可得出结论;
②根据方程的系数结合根的判别式,可得出△=-12<0,由此可得出原方程无实数根;
(2)根据一元二次方程的定义结合根的判别式,可得出关于m的一元一次不等式以及一元二次方程,解之即可得出结论.
解答 解:①∵x2+x-12=(x+4)(x-3)=0,
∴x+4=0或x-3=0,
解得:x1=-4,x2=3;
②∵△=b2-4ac=(-6)2-4×3×4=-12<0,
∴方程3x2-6x+4=0无实数根.
(2)∵关于x的一元二次方程(m-2)x2-4mx+2m-6=0有两个相等的实数根,
∴$\left\{\begin{array}{l}{m-2≠0}\\{△=(-4m)^{2}-4(m-2)(2m-6)=0}\end{array}\right.$,
解得:m1=1,m2=-6.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)①利用因式分解法,将x2+x-12=0变形为(x+4)(x-3)=0;②由△=-12<0,找出原方程无实数根;(2)根据一元二次方程的定义结合根的判别式,列出关于m的一元一次不等式以及一元二次方程.

练习册系列答案
相关题目
8.下列事件中是随机事件的是( )
| A. | 打开电视机正在播放欧洲杯 | |
| B. | 任意画一个三角形,其内角和为360° | |
| C. | 掷一枚质地均匀的骰子,掷出的点数为8 | |
| D. | 平行于同一条直线的两条直线平行 |
12.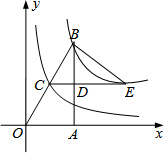 如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
 如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 与k1的值有关 |
13.有8张卡片,分别写着1、2、3、4、4、3、6、5的大小完全相同的数字卡片,将它们背面朝上洗均匀后任意抽出一张,结果抽到数字3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
 如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3.
如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3. 如图,六边形ABCDEF是正六边形,那么∠α的度数是60°.
如图,六边形ABCDEF是正六边形,那么∠α的度数是60°.