题目内容
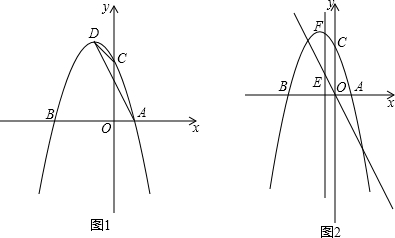
如图1,已知抛物线y=-x2+bx+c经过点A(1,0)和点C(0,3),该抛物线与x轴的另一个交点为B,顶点是D.
(1)求此抛物线的解析式和顶点D的坐标;
(2)求△ACD的面积;
(3)如图2,在直线y=-2x上有一动点E,过E作直线EF∥y轴,交该抛物线于点F,以E、F、C、O为顶点的四边形是平行四边形,求E点的坐标.
(1)求此抛物线的解析式和顶点D的坐标;
(2)求△ACD的面积;
(3)如图2,在直线y=-2x上有一动点E,过E作直线EF∥y轴,交该抛物线于点F,以E、F、C、O为顶点的四边形是平行四边形,求E点的坐标.

考点:二次函数综合题
专题:压轴题
分析:(1)利用待定系数法求二次函数解析式即可,再把函数解析式整理成顶点式形式,然后写出顶点D的坐标;
(2)利用待定系数法求出直线AD的解析式,设AD与y轴的交点为H,然后求出CD的长度,再利用三角形的面积公式列式计算即可得解;
(3)根据二次函数解析式与直线解析式表示出EF,然后根据平行四边形的对边平行且相等列方程求解即可.
(2)利用待定系数法求出直线AD的解析式,设AD与y轴的交点为H,然后求出CD的长度,再利用三角形的面积公式列式计算即可得解;
(3)根据二次函数解析式与直线解析式表示出EF,然后根据平行四边形的对边平行且相等列方程求解即可.
解答:解:(1)由题意得,
,
解得
,
所以,二次函数解析式是y=-x2-2x+3,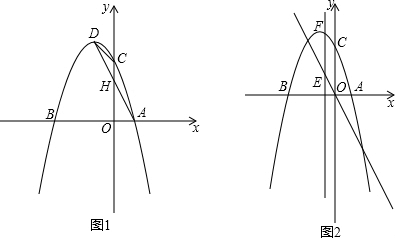
∵y=-x2-2x+3=-(x+1)2+4,
∴D点的坐标是(-1,4);
(2)设AD的解析式为y=kx+b,
则
,
解得
,
所以,直线AD的解析式为y=-2x+2,
设AD与y轴的交点为H,则CH=3-2=1,
所以,S△ACD=
×1×(1+1)=1;
(3)如图,设E点的坐标是(x,-2x),则F点的坐标是(x,-x2-2x+3),
EF=|-x2-2x+3+2x|=|x2-3|,
∵OC∥DE,
∴要使以F、E、C、O为顶点的四边形是平行四边形时,只要EF=OC,
∴|x2-3|=3,
∴x2-3=3或x2-3=-3,
解得x=±
,x=0(舍去),
当x=
时,y=-2x=-2
,
当x=-
时,y=-2x=2
,
所以,点E的坐标为(
,-2
)或(-
,2
).
|
解得
|
所以,二次函数解析式是y=-x2-2x+3,

∵y=-x2-2x+3=-(x+1)2+4,
∴D点的坐标是(-1,4);
(2)设AD的解析式为y=kx+b,
则
|
解得
|
所以,直线AD的解析式为y=-2x+2,
设AD与y轴的交点为H,则CH=3-2=1,
所以,S△ACD=
| 1 |
| 2 |
(3)如图,设E点的坐标是(x,-2x),则F点的坐标是(x,-x2-2x+3),
EF=|-x2-2x+3+2x|=|x2-3|,
∵OC∥DE,
∴要使以F、E、C、O为顶点的四边形是平行四边形时,只要EF=OC,
∴|x2-3|=3,
∴x2-3=3或x2-3=-3,
解得x=±
| 6 |
当x=
| 6 |
| 6 |
当x=-
| 6 |
| 6 |
所以,点E的坐标为(
| 6 |
| 6 |
| 6 |
| 6 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,三角形的面积,平行四边形的对边平行且相等的性质,难点在于(3)列出绝对值方程.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
下列说法中正确的是( )
| A、若a⊥b,b⊥c,则a⊥c |
| B、在同一平面内,不相交的两条线段必平行 |
| C、两条直线被第三条直线所截,所得的同位角相等 |
| D、两条平行线被第三条直线所截,一对内错角的角平分线互相平行 |
 如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是( )
如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是( )| A、15° | B、20° |
| C、22.5° | D、25° |
点P(3,m)到x轴的距离是4,则m的值为( )
| A、4 | B、±4 | C、-4 | D、无法确定 |
估计
-1的大小在( )
| 76 |
| A、5--6之间 |
| B、6--7之间 |
| C、7--8之间 |
| D、8--9之间 |
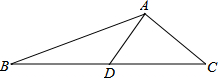 如图,在△ABC中,AB=5,AC=3,D为BC的中点,AD=2,则tan∠BAD=
如图,在△ABC中,AB=5,AC=3,D为BC的中点,AD=2,则tan∠BAD=