Question

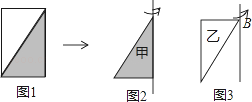
【题目】已知：如图，B、C分别是∠PAQ的两边AP，AQ上的点，直线l垂直平分BC。

（1）尺规作图：在直线1上求作一点O，使得点O到AP、AQ距离相等(不写作法，保留作图痕迹)；

（2）过O点作OE⊥AP，OF⊥AQ，垂足分别为E、F。求证BE=CF

Answer 1

【答案】（1）图见解析（2）见解析

【解析】

（1）根据题意作∠QAP的角平分线与l的交点即为O点；

（2）连接BO、CO，再根据角平分线上的点到角的两边距离相等可得OE=OF，根据线段垂直平分线上的点到两端点的距离相等可得BO=CO，然后利用“HL”证明Rt△BOE和Rt△COF全等，根据全等三角形对应边相等证明即可．

(1)如图所示，AO是∠QAP的角平分线，AO与l的交点即为所求O点；

(2)证明：连接BO、CO，

∵AO是∠BAC的平分线，

∴OE=OF，

∵l是BC边的垂直平分线，

∴BO=CO，

在Rt△BOE和Rt△COF中，

∴Rt△BOE≌Rt△COF(HL)，

∴BE=CF.