题目内容
如图所示,请你探索正方形的个数与等腰三角形的个数之间的关系.

(1)照这样的画法,如果画15个正方形,可以得
(2)若要得到152个等腰三角形,应画

(1)照这样的画法,如果画15个正方形,可以得
56
56
个等腰三角形;(2)若要得到152个等腰三角形,应画
39
39
个正方形;分析:从图中所给出的四个例子可知,当正方形个数为1时,等腰三角形的个数为0,当正方形的个数为2时,等腰三角形的个数为4,当正方形个数为3时,等腰三角形的个数为8,当正方形的个数为4时,等腰三角形的个数为12,从而可以得出规律当正方形的个数为n时,等腰三角形的个数为4(n-1).
解答:解:从图中可以得出如下规律:当正方形的个数为n时,等腰三角形的个数为4(n-1).
(1)当正方形的个数为15时,等腰三角形的个数为4(15-1)=56;
(2)由题意可知当正方形的个数为n时,等腰三角形的个数为4(n-1).
∴4(n-1)=152,可得n=39.
(1)当正方形的个数为15时,等腰三角形的个数为4(15-1)=56;
(2)由题意可知当正方形的个数为n时,等腰三角形的个数为4(n-1).
∴4(n-1)=152,可得n=39.
点评:本题考查同学们看图的能力,解题的关键是找出其中的规律.了解等腰三角形的性质.

练习册系列答案
相关题目
| |||||||||||||||
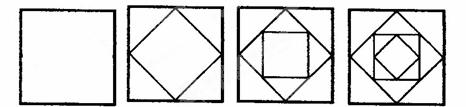
(1)如图所示,请你探索正方形与等腰三角形的个数之间的关系后填下表。
|
| 11 1 | 22 2 | 33 3 | 44 4 | ·· |
| 等 等腰三角形个数 | 0 | · ··· |
(2)若正方形的个数为n时,等腰三角形有___________ 个。
(3)若要得到152个等腰三角形,应画_____________个正方形;