题目内容
【题目】在平面内，C为线段AB外的一点，若以A，B，C为顶点的三角形为直角三角形，则称C为线段AB的直角点. 特别地，当该三角形为等腰直角三角形时，称C为线段AB的等腰直角点．
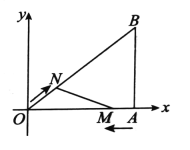
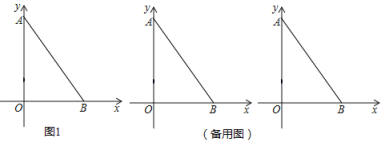
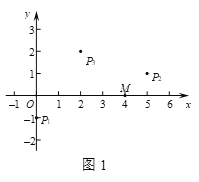
（1）如图1，在平面直角坐标系xOy中，点M的坐标为
，在点P1
，P2
，P3
中，线段OM的直角点是 ；
（2）在平面直角坐标系xOy中，点A，B的坐标分别为
，
，直线l的解析式为
．
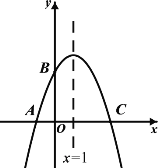
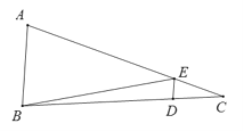
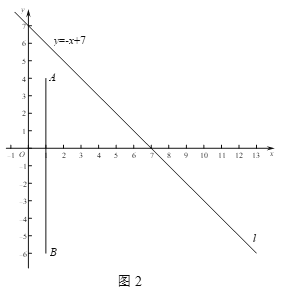
①如图2，C是直线l上的一个动点，若C是线段AB的直角点，求点C的坐标；
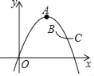
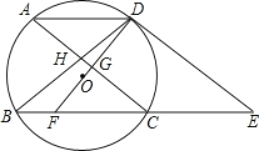
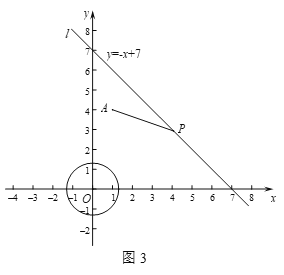
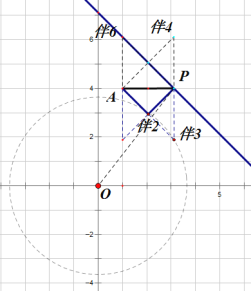
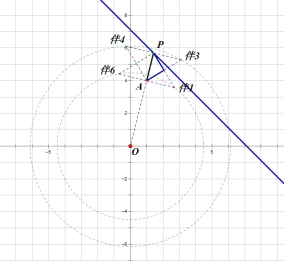
②如图3，P是直线l上的一个动点，将所有线段AP的等腰直角点称为直线l关于点A的伴随点.若⊙O的半径为r，且⊙O上恰有两个点为直线l关于点A的伴随点，直接写出r的取值范围．
【答案】（1）P1, P3；
（2）①点C的坐标为
或
或
或
；②
【解析】
根据直角点的定义判定即可.
（2）① ∠BAC=90°时，可设点C的坐标为（a，b）.
因为点A的坐标已知 ，点C在直线 上,可解得点C的坐标.
已知点B坐标同理可解点C坐标.
取AB的中点M，作CH⊥AB于点H，连接CM.
求出M坐标，算得CM长，在直角三角形CHM中利用勾股定理求得点C坐标.
② 关于r的取值范围根据图直接写出即可.
解：（1）根据直角点的定义线段OM的直角点为 P1, P3 ；
（2）① 当∠BAC=90°时，设点C的坐标为（a，b）.
∵点A的坐标为
，点C在直线
上,
∴ b=4，
，解得a=3.
∴点C的坐标为.
当∠ABC=90°时，设点C的坐标为（a，b）.
∵点B的坐标为
，点C在直线上,
∴ b=
，，解得a=13.
∴点C的坐标为.
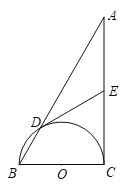
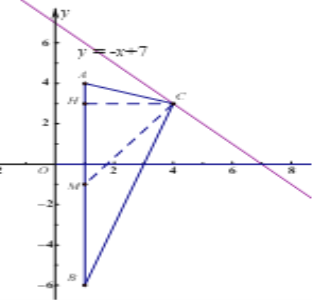
当∠ACB=90°时如图，设点C的坐标为（a, b）.
取AB的中点M，作CH⊥AB于点H，连接CM.
∵ 点C在直线上，
∴ 得. （*）
∵点A，B的坐标分别为，,
∴ 点M的坐标为
，CM=5，
.
∴ 由勾股定理得方程 
. （**）
由（*），（**）得
或
，故C的坐标为或.
综上，点C的坐标为或或或.
②如图AP与x轴平行时伴2、伴3共圆，r=
当O、A、P三点共线时伴3、伴4共圆r=O伴3=
即
直接写出r的取值范围是：
