题目内容

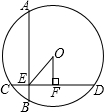如图，⊙O的弦AB⊥CD于E，OF⊥CD于F，且OF=2，OE=4，OA= $数学公式$ ．
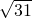（1）求AB的长；
（2）求BE的长．

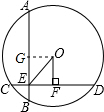解：（1）过点O作OG⊥AB于G，连接OA，则AG=BG= $\text{[math]}$ AB，
∵OF⊥CD，AB⊥CD，
∴∠OGE=∠OFE=∠FEG=90°，
∴四边形OFEG是矩形，
∴OG=EF，EG=OF，
在Rt△OEF中，EF= 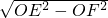$\text{[math]}$ = $\text{[math]}$ =2 $\text{[math]}$
∴OG=2 $\text{[math]}$ ，
在Rt△OAG中，AG= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
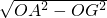∴AB=2 $\text{[math]}$ ．

（2）∵由（1）得，四边形OFEG是矩形，
∴EG=OF=2，
∵由（1）得，BG=AG= $\text{[math]}$ AB= $\text{[math]}$ ×2 $\text{[math]}$ = $\text{[math]}$ ，
∴BE=BG-EG= $\text{[math]}$ -2．
分析：（1）过点O作OG⊥AB于G，连接OA，则AG=BG= $\text{[math]}$ AB，再根据OF⊥CD，AB⊥CD可知四边形OFEG是矩形，再在Rt△OEF、Rt△OAG中利用勾股定理可求出EF及AG的长，故可得出AB的长；
（2））由（1）得，四边形OFEG是矩形，所以EG=OF=2，再由由（1）得，BG=AG= $\text{[math]}$ AB可得出BG的长，再根据BE=BG-EG即可得出结论．
点评：本题考查的是垂径定理、勾股定理及矩形的判定与性质，根据题意作出辅助线，构造出矩形及直角三角形是解答此题的关键．