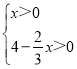Question

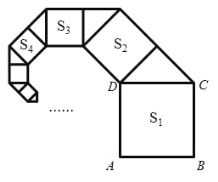
【题目】如图，正方形 ABCD 的边长为1，其面积为 S1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为 S2，…，按此规律继续下去，则 S9的值为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

根据等腰直角三角形的性质可得出S2+S2=S1，写出部分Sn的值，根据数的变化找出变化规律Sn=（）n-1，依此规律即可得出结论．

解：在图中标上字母E，如图所示．

∵正方形ABCD的边长为1，△CDE为等腰直角三角形，
∴DE2+CE2=CD2，DE=CE，
∴S2+S2=S1．
观察，发现规律：S1=12=1，S2=S1=，S3=S2=，S4=S3=，…，
∴Sn=（）n-1．
当n=9时，S9=（）9-1=（）8，
故选：B．