��Ŀ����
����Ŀ����ͼ������M��Nͬʱ��ԭ������������������˶�����֪����M��N���˶��ٶȱ���1��2���ٶȵ�λ��1����λ����/�룩�����˶�ʱ��Ϊt�룮
![]()
��1��������M�����Ḻ�����˶�������N�������������˶�����t=2��ʱ������M�˶���A�㣬����N�˶���B�㣬��AB=12����λ���ȣ���
����ֱ��l�ϻ���A��B�����λ�ã����ش𣺵�A�˶����ٶ����� ������λ����/�룩����B�˶����ٶ����� ������λ����/�룩��
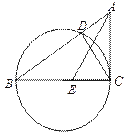
������PΪ������һ�㣬��PA��PB=OP����![]() ��ֵ��
��ֵ��
��2���ɣ�1����A��B�����λ�ÿ�ʼ����M��Nͬʱ�ٴο�ʼ��ԭ���˶������������ϵ��˶������ޣ��پ������룬MN=4����λ���ȣ���
���𰸡���1����2��4����4����2��4��8��![]() ��
��![]() ��
��
�������������������1���ٰ�A��B�����ʾ�������ϣ������M��N������ٶȼ��ɣ�
�����P�������϶�Ӧ����Ϊx������PA-PB=OP����x�ķ�Χ������ɣ�
��2�����پ���m�룬�ɵ�MN=4����λ���ȣ�����M��Nͬ���뷴��������ɣ�
�����������1���ٻ������ᣬ��ͼ��ʾ��
![]()
�ɵõ�M�˶����ٶ���2����λ����/�룩����N�˶����ٶ���4����λ����/�룩��
�ʴ�Ϊ��2��4��
�����P�������϶�Ӧ����Ϊx��
��PA��PB=OP��0��
��x��2��
��2��x��8ʱ��PA��PB=��x+4������8��x��=x+4��8+x����2x��4=x����ʱx=4��
��x��8ʱ��PA��PB=��x+4������x��8��=12����ʱx=12��
��![]() ��
��![]() ��
��
��2�����پ���m�룬�ɵ�MN=4����λ���ȣ���
��M��N�˶��ķ�����ͬ��Ҫʹ��MN=4����ΪN��M��
��|��8��4m��������4��2m��|=4����|12��2m|=4��
��ã�m=4��m=8��
��M��N�˶������෴��Ҫʹ��MN=4����ΪM��N������У�
��|��8��4m��������4+2m��|=4����|12��6m|=4��
��ã�m=![]() ��m=
��m=![]() ��
��
���ϣ�m=4��m=8��m=![]() ��m=
��m=![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�