题目内容
如图,直线经过A(1,0),B(0,1)两点,点P是双曲线y=| 1 | 2x |
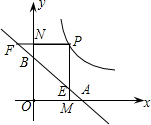 ⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.
⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.(1)求证:AF•BE=1;
(2)若平行于AB的直线与双曲线只有一个公共点,求公共点的坐标.
分析:(1)过点E、F分别作y轴、x轴的垂线,垂足为D、C,将求线段AF、BE的问题转化到等腰直角三角形△FCA,△DBE中求斜边的长,再做乘法,利用点P(x0,y0)在双曲线y=
上,列式求解;
(2)由A、B两点坐标可知,直线AB解析式的一次项系数为-1,平行于AB的直线l的解析式为y=-x+b,将直线l的解析式与双曲线解析式联立,消去y,得到关于x的一元二次方程,当l与双曲线的唯一公共点时,△=0求b的值即可.
| 1 |
| 2x |
(2)由A、B两点坐标可知,直线AB解析式的一次项系数为-1,平行于AB的直线l的解析式为y=-x+b,将直线l的解析式与双曲线解析式联立,消去y,得到关于x的一元二次方程,当l与双曲线的唯一公共点时,△=0求b的值即可.
解答: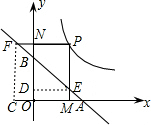 (1)证明:过点E、F分别作y轴、x轴的垂线,垂足为D、C,
(1)证明:过点E、F分别作y轴、x轴的垂线,垂足为D、C,
则△AOB,△FCA,△DBE为等腰直角三角形,
设P(x0,y0),则FC=y0,DE=x0,AF=
y0,BE=
x0,
∴AF•BE=
y0•
x0=2x0y0,
又y0=
,
即2x0y0=1,
∴AF•BE=1;
(2)解:平行于AB的直线l的解析式为y=-x+b,设l与双曲线的唯一公共点Q坐标为(x,y),
联立
,得2x2-2bx+1=0,
由△=4b2-8=0,得b=
(-
舍去),
∴x=
,y=
,
即Q点的坐标为(
,
).
 (1)证明:过点E、F分别作y轴、x轴的垂线,垂足为D、C,
(1)证明:过点E、F分别作y轴、x轴的垂线,垂足为D、C,则△AOB,△FCA,△DBE为等腰直角三角形,
设P(x0,y0),则FC=y0,DE=x0,AF=
| 2 |
| 2 |
∴AF•BE=
| 2 |
| 2 |
又y0=
| 1 |
| 2x0 |
即2x0y0=1,
∴AF•BE=1;
(2)解:平行于AB的直线l的解析式为y=-x+b,设l与双曲线的唯一公共点Q坐标为(x,y),
联立
|
由△=4b2-8=0,得b=
| 2 |
| 2 |
∴x=
| ||
| 2 |
| ||
| 2 |
即Q点的坐标为(
| ||
| 2 |
| ||
| 2 |
点评:此题主要考查反比例函数的性质,告诉我们注意通过解方程组求出交点坐标,同时要注意运用数形结合的思想.

练习册系列答案
相关题目
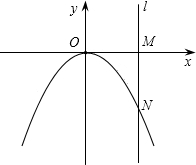 如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( )
如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( )A、
| ||
B、-
| ||
C、
| ||
D、-
|
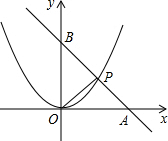 如图,直线l经过点A(4,0)和点B(0,4),且与二次函数y=ax2的图象在第一象限内相交于点P,若△AOP的面积为
如图,直线l经过点A(4,0)和点B(0,4),且与二次函数y=ax2的图象在第一象限内相交于点P,若△AOP的面积为 如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.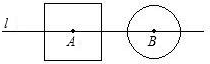 如图,直线l经过边长为10的正方形中心A,且与正方形的一组对边平行,⊙B的圆心B在直线l上,半径为r,AB=7,要使⊙B和正方形的边有2个公共点,那么r的取值范围是
如图,直线l经过边长为10的正方形中心A,且与正方形的一组对边平行,⊙B的圆心B在直线l上,半径为r,AB=7,要使⊙B和正方形的边有2个公共点,那么r的取值范围是 (2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y=
(2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y=