题目内容
点A的坐标（x，y）满足条件（x-3）2+|y+2|=0，则点A的位置在
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
D
分析：根据非负数的性质先判断出点的横纵坐标的符号，进而判断点所在的象限．
解答：∵（x-3）2≥0，|y+2|≥0，已知（x-3）2+|y+2|=0，
∴x-3=0，y+2=0，
∴x=3，y=-2．
则点A（3，-2）的位置在第四象限．
故选D．
点评：本题考查了非负数的性质：任何数的平方大于或等于0，任何数的绝对值大于或等于0；以及平面直角坐标系中各象限内的点的符号特点．
分析：根据非负数的性质先判断出点的横纵坐标的符号，进而判断点所在的象限．
解答：∵（x-3）2≥0，|y+2|≥0，已知（x-3）2+|y+2|=0，
∴x-3=0，y+2=0，
∴x=3，y=-2．
则点A（3，-2）的位置在第四象限．
故选D．
点评：本题考查了非负数的性质：任何数的平方大于或等于0，任何数的绝对值大于或等于0；以及平面直角坐标系中各象限内的点的符号特点．
练习册系列答案
名校课堂系列答案
相关题目
12、如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M，N两点，若点M的坐标是（-4，-2），则点N的坐标为（ ）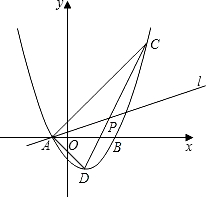
顶点，O为坐标原点．若OA、OB（OA＜OB）的长分别是方程x2-4x+3=0的两根，且∠DAB=45°．
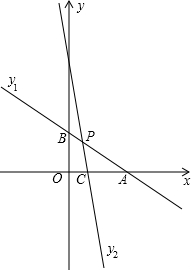0）经过点C（1，0）且与线段AB交于点P，并把△ABO分成两部分．
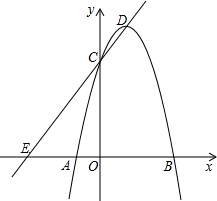如图，在平面直角坐标系中，抛物线y=-2x2+4x+6与x轴交于A、B两点（A点在B点左侧），与y轴交于C点，顶点为D．过点C、D的直线与x轴交于E点，以OE为直径画⊙O1，交直线CD于P、E两点．