题目内容
4.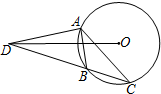 如图,△ABC内接于⊙O,∠ACB=30°,在CB的延长线上取一点D,使得AD=AC,若⊙O的半径等于1,则OD的长不可能为( )
如图,△ABC内接于⊙O,∠ACB=30°,在CB的延长线上取一点D,使得AD=AC,若⊙O的半径等于1,则OD的长不可能为( )| A. | 3 | B. | 2.5 | C. | 2 | D. | 1.5 |
分析 连接OA、OB,作△ABD的直径AE,连接BE,根据题意判断△AOB是等边三角形,求出AB=1,根据直角三角形的性质计算即可.
解答 解: 连接OA、OB,作△ABD的直径AE,连接BE,
连接OA、OB,作△ABD的直径AE,连接BE,
∵∠ACB=30°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=0A=1,
∵AD=AC,∠ACB=30°,
∴∠ACB=30°,
∴AE=2AB=2,
∴OD<1+2,即OD<3,
故选:A.
点评 本题考查的是相交两圆的性质,掌握圆周角定理、等边三角形的性质定理以及含30°的直角三角形的性质是解题的关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
17.在下列各选项中给出的三条线段不一定能组成三角形的是( )
| A. | a+1,a+2,a+3(a>0) | B. | 三条线段的比是4:6:8 | ||
| C. | 3cm,8cm,10cm | D. | 3a,5a,2a+1(a>0) |
16. 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )| A. | 相等 | B. | 互余 | C. | 互补 | D. | 无法确定 |
 如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.
如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.