��Ŀ����
����Ŀ���ۺ���
��1������
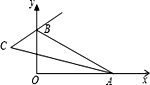
��ͼ���� ![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
�� ![]() .
.
��գ����� ![]() λ��ʱ���߶�
λ��ʱ���߶� ![]() �ij�ȡ�����ֵ�������ֵΪ.���ú�
�ij�ȡ�����ֵ�������ֵΪ.���ú� ![]() ��
�� ![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��2��Ӧ��
�� ![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
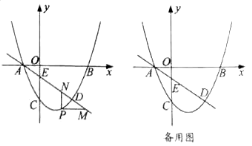
�� ![]() .��ͼ��ʾ���ֱ���
.��ͼ��ʾ���ֱ��� ![]() ��
�� ![]() Ϊ�ߣ����ȱ�������
Ϊ�ߣ����ȱ������� ![]() �͵ȱ�������
�͵ȱ������� ![]() ������
������ ![]() ��
�� ![]() .
.
���ҳ�ͼ���� ![]() ��ȵ��߶Σ���˵�����ɣ�
��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶� ![]() �������ֵ.
�������ֵ.
��3����չ
��ͼ����ƽ��ֱ������ϵ�У��� ![]() ������Ϊ
������Ϊ ![]() ����
���� ![]() ������Ϊ
������Ϊ ![]()
![]() Ϊ�߶�
Ϊ�߶� ![]() ��һ���㣬��
��һ���㣬�� ![]() ��
�� ![]() ��
�� ![]() �����߶�
�����߶� ![]() �������ֵ����ʱ��
�������ֵ����ʱ�� ![]() ������.
������.
���𰸡�
��1��CB���ӳ�����,a+b
��2���⣺��DC=BE,�������£�
�ߡ�ABD�͡�ACEΪ�ȱ������Σ�
��AD=AB,AC=AE,��BAD=��CAE=60�㣬
���BAD+��BAC=��CAE+��BAC������CAD=��EAB,
���CAD�ա�EAB.
��DC=BE.
��BE�����ֵ��4.
��3���⣺��ͼ3��
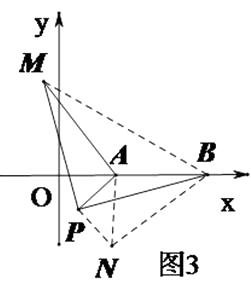
�����BNP�ա�MAP,��NB=AM,�ɣ�1��֪������N��BA���ӳ�����ʱ��NB�����ֵ���籸��ͼ����
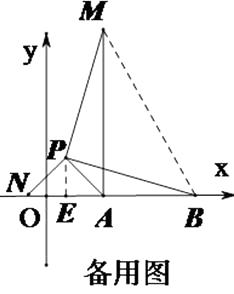
�á�APN�ǵ���ֱ�������Σ�AP=2����AN= ![]() ����AM=NB=AB+AN=3+
����AM=NB=AB+AN=3+ ![]() ;����P��PE��x���ڵ�E��PE=AE=
;����P��PE��x���ڵ�E��PE=AE= ![]() ,��A��2��0����P��2-
,��A��2��0����P��2- ![]() ��
�� ![]() ��
��
����������1������A���߶�CB���ӳ�����ʱ���ɵ��߶�AC�ij�ȡ�����ֵΪa+b��
��1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ����ۡ�
��2���ٸ��ݵȱ������ε����ʵõ�AD=AB��AC=AE����BAD=��CAE=60�㣬�Ƴ���CAD�ա�EAB������ȫ�������ε����ʵõ�CD=BE���������߶�BE�������ֵ=�߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ������
��3������BM������APM���ŵ�P˳ʱ����ת90��õ���PBN������AN���õ���APN�ǵ���ֱ�������Σ�����ȫ�������ε����ʵ�PN=PA=2��BN=AM�����ݵ�N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ�����ɵõ����ֵ����ͼ2����P��PE��x����E�����ݵ���ֱ�������ε����ʼ��ɵõ����ۣ�