题目内容
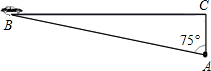 超速行驶是引发交通事故的主要原因之一.上周末,四位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离迎宾大道(60千米/小时的限制速度)的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,
超速行驶是引发交通事故的主要原因之一.上周末,四位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离迎宾大道(60千米/小时的限制速度)的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,| 3 |
考点:解直角三角形的应用
专题:
分析:由于A到BC的距离为30米,可见∠C=90°,根据75°角的三角函数值求出BC的距离;根据速度=路程÷时间即可得到汽车的速度,与60千米/小时进行比较即可.
解答:解:在Rt△ABC中,∠ACB=90°,∠BAC=75°,AC=30米,
则BC=AC•tan∠BAC=30×tan75°≈30×3.732≈112(米).
此车速度为:112÷8=14(米/秒)<16.7 (米/秒)=60(千米/小时)
所以,此车没有超过限制速度.
故答案是:否.
则BC=AC•tan∠BAC=30×tan75°≈30×3.732≈112(米).
此车速度为:112÷8=14(米/秒)<16.7 (米/秒)=60(千米/小时)
所以,此车没有超过限制速度.
故答案是:否.
点评:本题考查了解直角三角形的应用,理解正切函数的意义是解题的关键.

练习册系列答案
相关题目
如图的几何图形中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
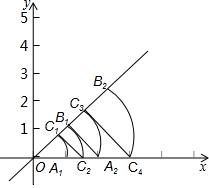 如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记
如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记 |
| A1C1 |
 |
| B1C2 |
 |
| A2C3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分式
与
的最简公分母是( )
| a |
| xy |
| b |
| yz |
| A、abxyz |
| B、abxy2z |
| C、xyz |
| D、xy2z |
 如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.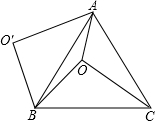 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论: