题目内容
一个等边三角形的边长、外接圆半径、内切圆半径之比是________．
2
分析：由等边三角形的边长、外接圆半径、内切圆半径正好组成一个直角三角形，从而求得它们的比．
解答：设等边三角形的边长为a，
∴所求的比为a：
，
故答案为2．
点评：本题考查了等边三角形的性质、三角形的内切圆和三角形的外接圆，是综合题，比较重要．
分析：由等边三角形的边长、外接圆半径、内切圆半径正好组成一个直角三角形，从而求得它们的比．
解答：设等边三角形的边长为a，
∴所求的比为a：
，故答案为2
．点评：本题考查了等边三角形的性质、三角形的内切圆和三角形的外接圆，是综合题，比较重要．
练习册系列答案
相关题目
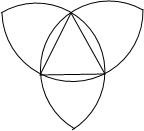已知一个等边三角形的边长为2，分别以它的三个顶点为圆心，边长为半径画弧，得到右图，那么图中所有的弧长的和是（ ）| A、4π | B、6π | C、8π | D、10π |
11、如图，一个等边三角形的边长与和它的一边相切的圆的周长相等，当此圆按箭头方向从某一位置沿等边三角形的三边作无滑动滚动，直至回到原出发位置时，则该圆转了（ ）
边形DEFG即为所求．