题目内容

一个等边三角形的边长为4，则这个等边三角形的面积为
 
．
分析：作出等边三角形边上高，利用60°的正弦值可得高的值，利用三角形的面积公式求解即可．
解答：精英家教网解：如图，作AD⊥BC于点D．
∴AD=AB×sin∠B=
3
2
×4=2
3
，
∴边长为a的等边三角形的面积为
1
2
×4×2
3
=4
3
，故答案为4
3
．
点评：考查三角形的面积的求法；利用60°的正弦值得到等边三角形一边上的高是解决本题的突破点．
练习册系列答案
相关题目
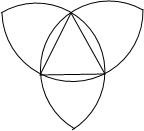精英家教网已知一个等边三角形的边长为2，分别以它的三个顶点为圆心，边长为半径画弧，得到右图，那么图中所有的弧长的和是（　　）
A、4πB、6πC、8πD、10π
11、如图，一个等边三角形的边长与和它的一边相切的圆的周长相等，当此圆按箭头方向从某一位置沿等边三角形的三边作无滑动滚动，直至回到原出发位置时，则该圆转了（　　）
△ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F、G分别落在AC、AB上．
Ⅰ、证明：△BDG≌△CEF；
Ⅱ、探究：怎样在铁片上准确地画出正方形．
小聪和小明各给出了一种想法，请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答．如果两题都解，只以Ⅱa的解答记分．
Ⅱa、小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了．
设△ABC的边长为2，请你帮小聪求出正方形的边长．（结果用含根号的式子表示，不要求分母有理化）
Ⅱb、小明想：不求正方形的边长也能画出正方形．具体作法是：
①在AB边上任取一点G′，如图作正方形G′D′E′F′；
②连接BF′并延长交AC于F；
③作FE∥F′E′交BC于E，FG∥F′G′交AB于G，GD∥G′D′交BC于D，则四精英家教网边形DEFG即为所求．
你认为小明的作法正确吗？说明理由．
一个等边三角形的边长为
2
，则其面积为
3
2
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网