题目内容
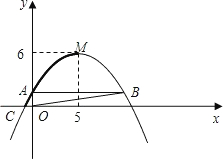
已知抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B，若点C在抛物线的对称轴上，点D在抛物线上，且以O，C，D，B四点为顶点的四边形为平行四边形，则D点的坐标为（6，-3）或（-2，-3）或（2，1）
（6，-3）或（-2，-3）或（2，1）
．分析：首先求出BO的长度进而求出D点横坐标，利用图象上点的坐标性质得出即可，再利用D点位置不同得出答案即可．
解答：解：
如图，当四边形OCDB是平行四边形时，CD=OB，
由0=-
（x-2）2+1得x1=0，x2=4，
∴B（4，0），OB=4．
由于对称轴x=2
∴D点的横坐标为6．
将x=6代入y=-
（x-2）2+1，得y=-3，
∴D（6，-3）；
根据抛物线的对称性可知，
在对称轴的左侧抛物线上存在点D，使得四边形ODCB是平行四边形，此时D点的坐标为（-2，-3），
当四边形OCBD是平行四边形时，D点即为A点，此时D点的坐标为（2，1）．
故答案为：（6，-3）或（-2，-3）或（2，1）．
如图，当四边形OCDB是平行四边形时，CD=OB，由0=-
| 1 |
| 4 |
∴B（4，0），OB=4．
由于对称轴x=2
∴D点的横坐标为6．
将x=6代入y=-
| 1 |
| 4 |
∴D（6，-3）；
根据抛物线的对称性可知，
在对称轴的左侧抛物线上存在点D，使得四边形ODCB是平行四边形，此时D点的坐标为（-2，-3），
当四边形OCBD是平行四边形时，D点即为A点，此时D点的坐标为（2，1）．
故答案为：（6，-3）或（-2，-3）或（2，1）．
点评：此题主要考查了二次函数的综合应用以及平行四边形的性质，根据已知得出D点不同位置是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
物线图象的一部分，如图中的粗线所示）在平移过程中所扫过的面积．
（2012•衡阳）如图所示，已知抛物线的顶点为坐标原点O，矩形ABCD的顶点A，D在抛物线上，且AD平行x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为（2，1），点P（a，b）在抛物线上运动．（点P异于点O）