题目内容
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1) 求证: AC平分∠DAB;
(2) 若点 为
为 的中点,
的中点,  ,AC=8,
,AC=8,
求AB和CE的长.
 |
(1)证明:连结OC.
∵直线CD与⊙O相切于点C, ∴OC⊥CD.
∵AD⊥CD, ∴OC∥AD. ∴∠DAC=∠ACO.
∵OA =OC ∴∠OAC=∠ACO.
 ∴∠DAC=∠CAO.即AC平分∠DAB. -
∴∠DAC=∠CAO.即AC平分∠DAB. -
(2)解:连接BC,
∵AB是⊙O的直径,∴∠ACB=90°=∠ADC.
∵∠DAC=∠CAO ,∴△ADC∽△ACB.
∴ .
.
∵ ,AC=8, ∴AB=10.
,AC=8, ∴AB=10.
∵点 为
为 的中点,∴∠ACE=45°.
的中点,∴∠ACE=45°.
过点A作CE的垂线,垂足为F,
∴CF =AF=ACsin45°= .
.
在Rt△ACB中, ,
,
∴ .
.
在Rt△AEF中, ,
,
∴ .
.
∴ .
.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目

 表示的实际意义是 .
表示的实际意义是 . ;
;  B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.

 中,
中, ,
, ;在
;在 中,
中, ,
, 。),点
。),点 为
为 的中点,
的中点, 交
交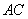 于点
于点 ,
, 经过点
经过点 。
。

 的度数;
的度数; 绕点
绕点 ,此时的等腰直角三角尺记为
,此时的等腰直角三角尺记为 ,
, 交
交 ,
, 交
交 于点
于点 ,试判断
,试判断 的值是否随着
的值是否随着 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出 (k是常数,k≠0),在其图像所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是(只需写一个).
(k是常数,k≠0),在其图像所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是(只需写一个).