题目内容
 在如图8×9的方格内,取A、B、C、D四个格点,使AB=BC=2CD=4,P是线段BC上的动点,连接AP、DP.
在如图8×9的方格内,取A、B、C、D四个格点,使AB=BC=2CD=4,P是线段BC上的动点,连接AP、DP.(1)设BP=a,用含字母a的代数式分别表示线段AP、DP的长;
(2)设k=AP+DP,k是否存在最小值?若存在,请求出其最小值;若不存在,请说明理由.
分析:(1)分别用a表示出BP、CD的长度,再根据勾股定理求出AP、DP的长即可;
(2)作点A关于BC的对称点A′,连接A′D,再由对称的性质及勾股定理即可求解.
(2)作点A关于BC的对称点A′,连接A′D,再由对称的性质及勾股定理即可求解.
解答: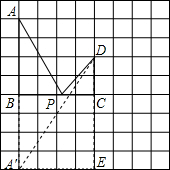 解:(1)由题意结合图形知:
解:(1)由题意结合图形知:
AB=4,BP=a,CP=4-a,CD=2,
∴AP=
=
,
DP=
=
=
;
(2)存在.
如图,作点A关于BC的对称点A′,连接A′D,
∴A′E=4,DE=6,
则A′D=
=
=
=2
.
故答案为:
、
、2
.
 解:(1)由题意结合图形知:
解:(1)由题意结合图形知:AB=4,BP=a,CP=4-a,CD=2,
∴AP=
| AB2+BP2 |
| a2+16 |
DP=
| PC2+CD2 |
| 22+(4-a)2 |
| a2-8a+20 |
(2)存在.
如图,作点A关于BC的对称点A′,连接A′D,
∴A′E=4,DE=6,
则A′D=
| A′E2+DE2 |
| 42+62 |
| 52 |
| 13 |
故答案为:
| a2+16 |
| a2-8a+20 |
| 13 |
点评:本题考查的是最短线路问题及勾股定理,根据题意画出图形是解答此类题目的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 21、画图题:
21、画图题: 一只蝴蝶在如图所示的方格形花坛上飞来飞去,最终落在阴影内的概率为
一只蝴蝶在如图所示的方格形花坛上飞来飞去,最终落在阴影内的概率为 在如图8×9的方格内,取A、B、C、D四个格点,使AB=BC=2CD=4,P是线段BC上的动点,连接AP、DP.
在如图8×9的方格内,取A、B、C、D四个格点,使AB=BC=2CD=4,P是线段BC上的动点,连接AP、DP.