题目内容
 已知,等边三角形ABC,D是AB上一点,DE⊥BC,垂足为E,EF⊥AC,垂足为F,FD⊥AB.
已知,等边三角形ABC,D是AB上一点,DE⊥BC,垂足为E,EF⊥AC,垂足为F,FD⊥AB.(1)说明△DEF 为等边三角形的理由;(2)若AD=2,试求△ABC和△DEF的面积.
分析:(1)由等边三角形ABC,DE⊥BC,FD⊥AB,根据平角的性质、垂直的定义即可推出∠EDF=60°,同样的道理推出∠DEF=60°,即可推出△DEF为等边三角形;
(2)根据(1)所推出的结论,结合全等三角形的判定定理“AAS”,即可得,△ADF≌△BED≌△CFE,再通过直角三角形中特殊角的三角函数,即可推出DF、DE、EF的长度,然后根据三角形的面积公式即可求出
(2)根据(1)所推出的结论,结合全等三角形的判定定理“AAS”,即可得,△ADF≌△BED≌△CFE,再通过直角三角形中特殊角的三角函数,即可推出DF、DE、EF的长度,然后根据三角形的面积公式即可求出
解答:解:(1)∵等边△ABC,
∴∠B=60°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=30°,
∵FD⊥AB,
∴∠ADF=90°,
∴∠EDF=60°,
同理,∠DEF=60°,
∴△DEF为等边三角形,
(2)∵△DEF为等边三角形,
∴DE=DF=EF,
∵∠DEB=∠ADF=∠EFC=90°,∠A=∠B=∠C=60°,
∴在△ADF和△BED中,
,
∴△ADF≌△BED(AAS),
∴同理,△ADF≌△BED≌△CFE,
∴AF=BD=EC,且AD=BE=CF,
∴AD=2,∠ADF=90°,∠A=60°,
∴AF=4,DF=2
,
∴AB=6,
∴AB=BC=AC=6,DF=DE=EF=2
,
过A作AM⊥BC于M,
则BM=MC=3,由勾股定理得:AM=3
,
∴S△ABC=
BC×AM=
×6×3
=9
,
同理S△DEF=
×2
×3=3
.
∴S△ABC=9
,S△DEF=3
.
∴∠B=60°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=30°,
∵FD⊥AB,
∴∠ADF=90°,
∴∠EDF=60°,
同理,∠DEF=60°,
∴△DEF为等边三角形,
(2)∵△DEF为等边三角形,

∴DE=DF=EF,
∵∠DEB=∠ADF=∠EFC=90°,∠A=∠B=∠C=60°,
∴在△ADF和△BED中,
|
∴△ADF≌△BED(AAS),
∴同理,△ADF≌△BED≌△CFE,
∴AF=BD=EC,且AD=BE=CF,
∴AD=2,∠ADF=90°,∠A=60°,
∴AF=4,DF=2
| 3 |
∴AB=6,
∴AB=BC=AC=6,DF=DE=EF=2
| 3 |
过A作AM⊥BC于M,
则BM=MC=3,由勾股定理得:AM=3
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
同理S△DEF=
| 1 |
| 2 |
| 3 |
| 3 |
∴S△ABC=9
| 3 |
| 3 |
点评:本题主要考查等边三角形的性质及判定,全等三角形的判定及性质,特殊角的三角函数,关键在于通过求相关角的度数推出△DEF为等边三角形,根据相关的定理求证相关的三角形全等,通过认真的计算求得三角形的三边长度.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
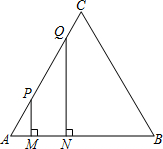 线段MN运动的时间为t秒.
线段MN运动的时间为t秒.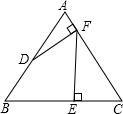 如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.
如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4. 17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.
17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE. 已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.
已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.