Question

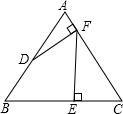如图，已知：等边三角形ABC，点D是AB的中点，过点D作DF⊥AC，垂足为F，过点F作FE⊥BC，垂足为E，若三角形ABC的边长为4．
求：（1）线段AF的长度；（2）线段BE的长度．

Answer 1

分析：（1）根据等边三角形各内角为60°的性质，可以求得∠ADF=30°，即可求得AD=2AF；
（2）根据与（1）同样的道理，即可求得CF=2CE，根据BE=BC-CE即可求的BE的长．

解答：解：（1）∵D是AB的中点，
∴AD=

AB

2

=2，
∵等边三角形ABC中∠A=∠C=60°，
且DF⊥AC，
∴∠ADF=180°-90°-60°=30°，
在Rt△ADF中，AF=

AD

2

=1；

（2）FC=AC-AF=4-1=3，
同理，在Rt△FEC中，EC=

FC

2

=1.5，
∴BE=BC-EC=4-1.5=2.5．
故答案为：AF=1，BE=2.5．

点评：本题考查了三角形各边长相等、各内角为60°的性质，30°角在直角三角形中运用，本题中根据特殊角的三角函数值求解是解题的关键．