题目内容
如图,在⊙O中,半径OC⊥弦AB于点D,AB= ,AO=4,则∠O= .
,AO=4,则∠O= .
【答案】分析:由半径OC与弦AB垂直,利用垂径定理得到D为AB的中点,由AB的长求出AD的长,在直角三角形AOD中,利用锐角三角函数定义求出sinO的值,利用特殊角的三角函数值即可求出∠O的度数.
解答:解:∵半径OC⊥弦AB,
∴D为AB的中点,又AB=4 ,
,
∴AD= AB=2
AB=2 ,
,
在Rt△AOD中,AO=4,AD=2 ,
,
∴sinO= =
= ,
,
又∵∠O为锐角,
∴∠O=60°.
故答案为:60°.
点评:此题考查了垂径定理,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握垂径定理是解本题的关键.
解答:解:∵半径OC⊥弦AB,
∴D为AB的中点,又AB=4
 ,
,∴AD=
 AB=2
AB=2 ,
,在Rt△AOD中,AO=4,AD=2
 ,
,∴sinO=
 =
= ,
,又∵∠O为锐角,
∴∠O=60°.
故答案为:60°.
点评:此题考查了垂径定理,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
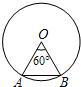 19、如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB=
19、如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB=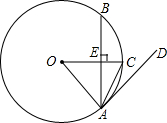 (2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E. (2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=
(2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=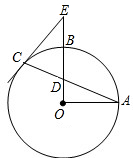 如图,在⊙O中,半径OA⊥OB,弦AC交OB于点D,E是OB延长线上一点,如果∠OAD=30°,ED=CE.
如图,在⊙O中,半径OA⊥OB,弦AC交OB于点D,E是OB延长线上一点,如果∠OAD=30°,ED=CE.