题目内容
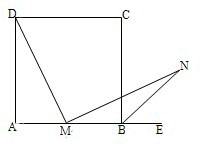24、如图，在正方形ABCD中，M为AB的中点，MN⊥MD，BN平分∠CBE并交MN于N．试说明：MD=MN．
分析：如图，将△BMN以∠DMN的角平分线为轴翻折至△PDM的位置，即取AD的中点P，连接PM．从而△MPD≌△NBM，故DM=MN．
解答：解：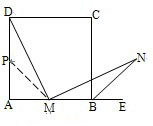
取AD的中点P，连接PM，
∵M为AB的中点，且四边形ABCD是正方形，
∴AB=CD；
∴AM=AP=BM=PD；
∴∠AMP=∠APM=45°；
∴∠DPM=135°；
而BN平分∠CBE，
∴∠NBE=45°；
∴∠MBN=135°；
∵MN⊥MD，
∴∠ADM+∠AMD=∠NMB+∠AMD=90°，
∴∠ADM=∠NMB；
∴△MPD≌△NBM，
∴DM=MN．
取AD的中点P，连接PM，∵M为AB的中点，且四边形ABCD是正方形，
∴AB=CD；
∴AM=AP=BM=PD；
∴∠AMP=∠APM=45°；
∴∠DPM=135°；
而BN平分∠CBE，
∴∠NBE=45°；
∴∠MBN=135°；
∵MN⊥MD，
∴∠ADM+∠AMD=∠NMB+∠AMD=90°，
∴∠ADM=∠NMB；
∴△MPD≌△NBM，
∴DM=MN．
点评：此题把正方形和全等三角形的知识结合起来，主要利用正方形的性质，全等三角形的性质与判定来解题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图：在正方形网格上有△ABC，△DEF，说明这两个三角形相似，并求出它们的相似比．
，交BC于点E．
23、如图，在Rt△ABC中，∠BAC=90°，AD=CD，点E是边AC的中点，连接DE，DE的延长线与边BC相交于点F，AG∥BC，交DE于点G，连接AF、CG．
如图，在Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6