题目内容
 如图,以数轴的单位长度1为边作正方形ABCO,其中点O是数轴原点,以点A为旋转中心,将AC逆时针旋转,使点C落在数轴负半轴的点D处,则点D表示的数是
如图,以数轴的单位长度1为边作正方形ABCO,其中点O是数轴原点,以点A为旋转中心,将AC逆时针旋转,使点C落在数轴负半轴的点D处,则点D表示的数是1-
| 2 |
1-
.| 2 |
分析:首先根据正方形的性质可得CO=AO=1,再根据勾股定理计算出AC的长,进而得到AD的长,然后可表示出点D表示的数.
解答:解:∵四边形ABCO是正方形,
∴AO=CO=1,∠COA=90°,
在Rt△ACO中,AC=
=
,
∵以点A为旋转中心,将AC逆时针旋转,使点C落在数轴负半轴的点D处,
∴AD=
,
∴DO=AD-AO=
-1,
∴点D表示的数是:-(
-1)=1-
,
故答案为:1-
.
∴AO=CO=1,∠COA=90°,
在Rt△ACO中,AC=
| CO2+AO2 |
| 2 |
∵以点A为旋转中心,将AC逆时针旋转,使点C落在数轴负半轴的点D处,
∴AD=
| 2 |
∴DO=AD-AO=
| 2 |
∴点D表示的数是:-(
| 2 |
| 2 |
故答案为:1-
| 2 |
点评:此题主要考查了勾股定理的应用、正方形的性质、以及实数与数轴,关键是计算出AC的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是
如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是
 如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是
如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是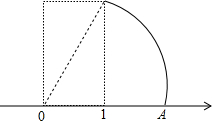 如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
如图,以数轴的单位长线段和单位长线段的两倍为边作一个长方形,以数轴的原点为圆心、长方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )