题目内容
120°、30°、30°的等腰三角形三边的比值是多少?36°、72°、72°的等腰三角形的三边的比值是多少?
考点:黄金分割
专题:计算题
分析:如图1,∠B=∠C=30°,∠BAC=120°,作AD⊥BC于D,设AD=a,易得△ABC为等腰三角形,根据等腰三角形的性质得BD=CD,AB=AC,在Rt△ABD中,利用含30度的直角三角形三边的关系得到AB=2a,BD=
a,BC=2BD=2
a,原式可计算出AB:AC:BC=1:1:
;
如图2,∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,易得图中三角形都是等腰三角形,设BC=x,AC=y,则AD=x,CD=y-x,易证得△BCD∽△ABC,
利用相似比可得x:y=(y-x):x,整理得x2+yx-y2=0,解方程得到x=
y,则可计算出BC:AB:AC=
:1:1.
| 3 |
| 3 |
| 3 |
如图2,∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,易得图中三角形都是等腰三角形,设BC=x,AC=y,则AD=x,CD=y-x,易证得△BCD∽△ABC,
利用相似比可得x:y=(y-x):x,整理得x2+yx-y2=0,解方程得到x=
-1+
| ||
| 2 |
| ||
| 2 |
解答:解:如图1,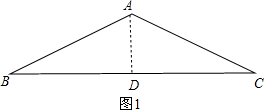 ∠B=∠C=30°,∠BAC=120°,
∠B=∠C=30°,∠BAC=120°,
作AD⊥BC于D,设AD=a,
∵∠B=∠C=30°,
∴△ABC为等腰三角形,
∴BD=CD,AB=AC,
在Rt△ABD中,AB=2a,BD=
a,
∴BC=2BD=2
a,
∴AB:AC:BC=2a:2a:2
a=1:1:
;
如图2,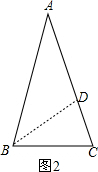 ∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,
∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,
∵∠ABC=∠ACB=72°,
∴AB=AC,
∵BD平分∠ABC,
∴∠ABD=36°,
∴DA=DB,
∵∠BDC=∠ABD+∠A=72°=∠C,
∴BD=BC,
∴AD=BC,
设BC=x,AC=y,则AD=x,CD=y-x,
易证得△BCD∽△ABC,
∴BC:AC=CD:BC,即x:y=(y-x):x,
整理得x2+yx-y2=0,解得x1=
y,x2=
y(舍去),
∴x=
y,
∴BC:AB:AC=x:y:y=
y:y:y=
:1:1.
答:120°、30°、30°的等腰三角形三边的比值为1:1:
;36°、72°、72°的等腰三角形的三边的比值是
:1:1.
 ∠B=∠C=30°,∠BAC=120°,
∠B=∠C=30°,∠BAC=120°,作AD⊥BC于D,设AD=a,
∵∠B=∠C=30°,
∴△ABC为等腰三角形,
∴BD=CD,AB=AC,
在Rt△ABD中,AB=2a,BD=
| 3 |
∴BC=2BD=2
| 3 |
∴AB:AC:BC=2a:2a:2
| 3 |
| 3 |
如图2,
 ∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,
∠ABC=∠ACB=72°,∠A=36°,作BD平分∠ABC,∵∠ABC=∠ACB=72°,
∴AB=AC,
∵BD平分∠ABC,
∴∠ABD=36°,
∴DA=DB,
∵∠BDC=∠ABD+∠A=72°=∠C,
∴BD=BC,
∴AD=BC,
设BC=x,AC=y,则AD=x,CD=y-x,
易证得△BCD∽△ABC,
∴BC:AC=CD:BC,即x:y=(y-x):x,
整理得x2+yx-y2=0,解得x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴x=
-1+
| ||
| 2 |
∴BC:AB:AC=x:y:y=
| ||
| 2 |
| ||
| 2 |
答:120°、30°、30°的等腰三角形三边的比值为1:1:
| 3 |
| ||
| 2 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.也考查了等腰三角形的性质.
| ||
| 2 |

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知:2a=-a,则数a等于( )
| A、不确定 | B、1 | C、-1 | D、0 |
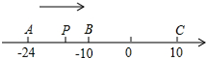 已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒. 如图,一张长方形纸片,按如图的分法折叠一角,折痕为EF,如果∠1=40°,试求∠2的度数.
如图,一张长方形纸片,按如图的分法折叠一角,折痕为EF,如果∠1=40°,试求∠2的度数.