题目内容
如图，用边长分别为1和3的两个正方形组成一个图形，则能将其完全覆盖的圆形纸片的最小半径为
- A.2
- B.2.5
- C.3
- D.
B
分析：根据已知得出当AB为⊙O的直径，此时圆形纸片半径最小，进而利用勾股定理求出即可．
解答：
解：如图所示：当AB为⊙O的直径，此时圆形纸片半径最小，
∵AC=3，BC=4，
∴AB=
=5，
∴能将其完全覆盖的圆形纸片的最小半径为：2.5．
故选：B．
点评：此题主要考查了圆的综合以及勾股定理，得出圆形纸片半径最小时图形是解题关键．
分析：根据已知得出当AB为⊙O的直径，此时圆形纸片半径最小，进而利用勾股定理求出即可．
解答：
解：如图所示：当AB为⊙O的直径，此时圆形纸片半径最小，∵AC=3，BC=4，
∴AB=
=5，∴能将其完全覆盖的圆形纸片的最小半径为：2.5．
故选：B．
点评：此题主要考查了圆的综合以及勾股定理，得出圆形纸片半径最小时图形是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
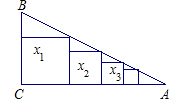已知△ABC是直角三角形，∠C=90°，BC=2，AC=5，如图那样把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，则第1个正方形的边长x1=
如图，用边长分别为1和3的两个正方形组成一个图形，则能将其完全覆盖的圆形纸片的最小半径为（ ）
长边与短边之比为2：1的长方形为“标准长方形”．约定用短边分别为a1、a2、a3、a4、a5（其中a1＜a2＜a3＜a4＜a5）的5个不同“标准长方形”拼成的大长方形记为（a1、a2、a3、a4、a5），如图，短边长分别为1，2，2.5，4.5，7的“标准长方形”拼成的大长方形记为（1，2，2.5，4.5，7），解答下列问题：