题目内容

若抛物线y=ax2+bx+c与x轴交于点A（0，0）、B（4，0），则抛物线的对称轴为直线
 
．
分析：将点A（0，0）、B（4，0）代入抛物线的解析式y=ax2+bx+c，得出方程组，再由对称轴的方程得出答案．
解答：解：将点A（0，0）、B（4，0）代入抛物线的解析式y=ax2+bx+c，
得
c=0
16a+4b+c=0
，
∴b=-4a，
∵抛物线的对称轴为x=-
b
2a
=-
-4a
2a
=2．
故答案为：x=2．
点评：本题考查了用待定系数法求二次函数的解析式，以及二次函数的性质．
练习册系列答案
相关题目
已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．
（1）求点C的坐标；
（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；
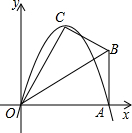
（3）若抛物线的对称轴与OB交于点D，点P为线段DB上一点，过P作y轴的平行线，交抛物线于点M精英家教网．问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(-
b
2a
，
4ac-b2
4a
)，对称轴公式为x=-
b
2a
．
若抛物线y=ax2+bx+c的开口向上，且经过原点，请写出符合上述条件的一个解析式
y=x2
y=x2
．
（2013•镇江模拟）已知抛物线y=ax2+bx经过点A（-3，-3）和点P（t，0），且t≠0．
（1）如图，若A点恰好是抛物线的顶点，请写出它的对称轴和t的值．
（2）若t=-4，求a、b的值，并指出此时抛物线的开口方向．
（3）若抛物线y=ax2+bx的开口向下，请直接写出t的取值范围．
（2013•平谷区一模）如图，在直角坐标系中，已知直线y=
1
2
x+1与y轴交于点A，与x轴交于点B，以线段BC为边向上作正方形ABCD．
（1）点C的坐标为
（-3，2）
（-3，2）
，点D的坐标为
（-1，3）
（-1，3）
；
（2）若抛物线y=ax2+bx+2（a≠0）经过C、D两点，求该抛物线的解析式；
（3）若正方形以每秒
5
个单位长度的速度沿射线BA向上平移，直至正方形的顶点C落在y轴上时，正方形停止运动．在运动过程中，设正方形落在y轴右侧部分的面积为s，求s关于平移时间t（秒）的函数关系式，并写出相应自变量t的取值范围．
若抛物线y=ax2+x+1（a≠0）的顶点始终在x轴的上方，则a的取值范围
a＞
1
4
或a＜0
a＞
1
4
或a＜0
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网