题目内容
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特征:甲:对称轴是![]() ;乙:与
;乙:与![]() 轴两个交点的横坐标都是整数;丙:与
轴两个交点的横坐标都是整数;丙:与![]() 轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为
轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为![]() .请写出满足上述全部特征的一个二次函数的解析式.
.请写出满足上述全部特征的一个二次函数的解析式.
【答案】![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
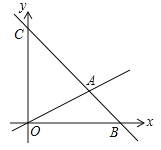
根据题意画出图形,直接写出图象与x轴交点的横坐标,根据以这三个点为顶点的三角形面积为3,求出与y轴交点纵坐标,当其值为正数时即可.
解:如图所示:令A点坐标为(3,0),
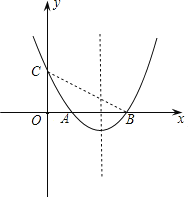
∵对称轴是x=4,
∴B点坐标为(5,0).
又∵△ABC的面积为3,
∴![]() ×AB×OC=3,即
×AB×OC=3,即![]() (5-3)
(5-3)![]() OC=3,解得OC=3,
OC=3,解得OC=3,
∴C点纵坐标为3,是整数,符合题意.
设二次函数解析式为y=a(x-3)(x-5),把C(0,3)代入解析式得:3=a(0-3)(0-5),解得a=![]() ,
,
∴函数解析式为y=![]() (x-3)(x-5),即y=
(x-3)(x-5),即y=![]() .
.
故答案为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目