题目内容
10.二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如下表:| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
(1)二次函数y=ax2+bx+c最小值为-4;
(2)若y<0,则x的取值范围是0<x<2;
(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧,则其中正确结论的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据表格中的x与y的对应值,确定出二次函数顶点坐标,以及与x轴的交点,即可作出判断.
解答 解:由表格得:二次函数顶点坐标为(1,-4),开口向上,与x轴交点坐标为(-1,0)与(3,0),
则(1)二次函数y=ax2+bx+c最小值为-4,正确;
(2)若y<0,则x的取值范围是-1<x<3,错误;
(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧,正确,
故选C
点评 此题考查了抛物线与x轴的交点,以及二次函数的性质,熟练掌握二次函数图象与性质是解本题的关键.

练习册系列答案
相关题目
20.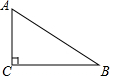 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
1.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为220元,按标价的五折销售,仍可获利10%,则这件商品的进价为( )
| A. | 120元 | B. | 100元 | C. | 80元 | D. | 60元 |
18.解方程$\frac{3x+2}{4}$-$\frac{5x+1}{12}$=1-$\frac{2x-1}{2}$时,去分母正确的是( )
| A. | 3(3x+2)-5x+1=12-6(2x-1) | B. | 3(3x+2)-5x-1=1-6(2x-1) | ||
| C. | 3(3x+2)-5x-1=12-6(2x-1) | D. | (3x+2)-5x+1=12-6(2x-1) |
5.点P位于y轴左侧,距y轴3个单位,且位于x轴下方,距x轴5个单位,则点P位的坐标为( )
| A. | (-3,-5) | B. | (-3,5) | C. | (5,-3) | D. | (-5,-3) |
15.九年级一班有七个学习小组,每组人数如下:5,5,6,x,6,7,8,已知平均每个小组有6个,则这组数据的众数与中位数分别是( )
| A. | 5,6 | B. | 6,5 | C. | 6,7 | D. | 5,8 |
2. 如图,在点B处测得A处的俯角是( )
如图,在点B处测得A处的俯角是( )
 如图,在点B处测得A处的俯角是( )
如图,在点B处测得A处的俯角是( )| A. | ∠1 | B. | ∠2 | C. | ∠3 | D. | ∠4 |
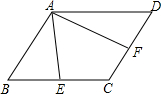 如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$.