Question

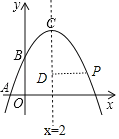
【题目】在平面直角坐标系xOy中（如图）．已知抛物线y=﹣x2+bx+c经过点A（﹣1，0）和点B（0，），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．

（1）求这条抛物线的表达式；

（2）求线段CD的长；

（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．

Answer 1

【答案】（1）抛物线解析式为y=﹣x2+2x+；（2）线段CD的长为2；（3）M点的坐标为（0，）或（0，﹣）．

【解析】（1）利用待定系数法求抛物线解析式；

（2）利用配方法得到y=﹣（x﹣2）2+，则根据二次函数的性质得到C点坐标和抛物线的对称轴为直线x=2，如图，设CD=t，则D（2，﹣t），根据旋转性质得∠PDC=90°，DP=DC=t，则P（2+t，﹣t），然后把P（2+t，﹣t）代入y=﹣x2+2x+得到关于t的方程，从而解方程可得到CD的长；

（3）P点坐标为（4，），D点坐标为（2，），利用抛物线的平移规律确定E点坐标为（2，﹣2），设M（0，m），当m＞0时，利用梯形面积公式得到（m++2）2=8当m＜0时，利用梯形面积公式得到（﹣m++2）2=8，然后分别解方程求出m即可得到对应的M点坐标．

（1）把A（﹣1，0）和点B（0，）代入y=﹣x2+bx+c得

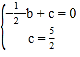，解得，

∴抛物线解析式为y=﹣x2+2x+；

（2）∵y=﹣（x﹣2）2+，

∴C（2，），抛物线的对称轴为直线x=2，

如图，设CD=t，则D（2，﹣t），

∵线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处，

∴∠PDC=90°，DP=DC=t，

∴P（2+t，﹣t），

把P（2+t，﹣t）代入y=﹣x2+2x+得﹣（2+t）2+2（2+t）+=﹣t，

整理得t2﹣2t=0，解得t1=0（舍去），t2=2，

∴线段CD的长为2；

（3）P点坐标为（4，），D点坐标为（2，），

∵抛物线平移，使其顶点C（2，）移到原点O的位置，

∴抛物线向左平移2个单位，向下平移个单位，

而P点（4，）向左平移2个单位，向下平移个单位得到点E，

∴E点坐标为（2，﹣2），

设M（0，m），

当m＞0时，（m++2）2=8，解得m=，此时M点坐标为（0，）；

当m＜0时，（﹣m++2）2=8，解得m=﹣，此时M点坐标为（0，﹣）；

综上所述，M点的坐标为（0，）或（0，﹣）．