题目内容
12. 如图,在⊙O中,∠OAB=45°,圆心O到弦AB的距离OE=2cm,则弦AB的长为4cm.
如图,在⊙O中,∠OAB=45°,圆心O到弦AB的距离OE=2cm,则弦AB的长为4cm.
分析 首先由垂径定理可知:AE=BE,然后再在Rt△AOE中,由特殊锐角三角函数可求得AE=OE=2,从而可求得弦AB的长.
解答 解:∵OE⊥AB,
∴AE=EB
在Rt△AOE中,∠OAB=45°,
∴tan∠OAB=$\frac{OE}{AE}=1$,
∴AE=OE=2.
∴AB=2AE=2×2=4.
故答案为:4cm.
点评 本题主要考查的是锐角三角函数和垂径定理的应用,掌握垂径定理和特殊锐角三角函数值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列式子:2a2b,3xy-2y2,$\frac{a+b}{2}$,4,-m,$\frac{x+yz}{2x}$,$\frac{ab-c}{π}$,其中是多项式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.下列方程中,没有实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-3=0 |
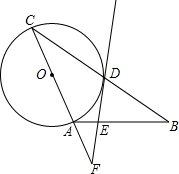 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. 如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.