题目内容
如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.
(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
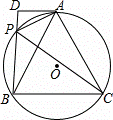
(1)证明:作⊙O的直径AE,连接PE,
∵AE是⊙O的直径,AD是⊙O的切线,
∴∠DAE=∠APE=90°,
∴∠PAD+∠PAE=∠PAE+∠E=90°,
∴∠PAD=∠E,
∵∠PBA=∠E,∴∠PAD=∠PBA,
∵∠PAD=∠PBA,∠ADP=∠BDA,
∴△ADP∽△BDA;
(2)PA+PB=PC,
证明:在线段PC上截取PF=PB,连接BF,
∵PF=PB,∠BPC=60°,
∴△PBF是等边三角形,
∴PB=BF,∠BFP=60°,
∴∠BFC=180°﹣∠PFB=120°,
∵∠BPA=∠APC+∠BPC=120°,
∴∠BPA=∠BFC,
在△BPA和△BFC中, ,
,
∴△BPA≌△BFC(AAS),
∴PA=FC,AB=BC,
∴PA+PB=PF+FC=PC;
(3)解:∵△ADP∽△BDA,
∴ =
= =
= ,
,
∵AD=2,PD=1
∴BD=4,AB=2AP,
∴BP=BD﹣DP=3,
∵∠APD=180°﹣∠BPA=60°,
∴∠APD=∠APC,
∵∠PAD=∠E,∠PCA=∠E,
∴PAD=∠PCA,
∴△ADP∽△CAP,
∴ =
= ,
,
∴AP2=CP•PD,
∴AP2=(3+AP)•1,
解得:AP= 或AP=
或AP= (舍去),
(舍去),
∴BC=AB=2AP=1+ .
.


下列说法正确的是( )
|
| A. | “明天降雨的概率是50%”表示明天有半天都在降雨 |
|
| B. | 数据4,4,5,5,0的中位数和众数都是5 |
|
| C. | 要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式 |
|
| D. | 若甲、乙两组数中各有20个数据,平均数 |
已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
| x | ﹣1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | ﹣1 | ﹣1 | 1 |
则该二次函数图象的对称轴为( )
|
| A. | y轴 | B. | 直线x= | C. | 直线x=2 | D. | 直线x= |
如图是某个几何体的三视图,则该几何体的形状是( )

|
| A. | 长方体 | B. | 圆锥 | C. | 圆柱 | D. | 三棱柱 |


 的范围.
的范围. ,且
,且 ,求m.
,求m. ÷
÷ = .
= .
 =
= ,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定

