题目内容
在Rt△ABC中,∠A=90°,D、E分别为AB、AC上的点.
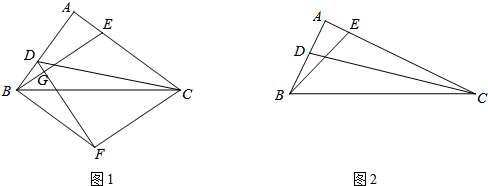
(1)如图1,CE=AB,BD=AE,过点C作CF∥EB,且CF=EB,连接DF交EB于点G,连接BF,请你直接写出
的值;
(2)如图2,CE=kAB,BD=kAE,
=
,求k的值.

(1)如图1,CE=AB,BD=AE,过点C作CF∥EB,且CF=EB,连接DF交EB于点G,连接BF,请你直接写出
| EB |
| DC |
(2)如图2,CE=kAB,BD=kAE,
| EB |
| DC |
| 1 |
| 2 |
考点:相似形综合题
专题:压轴题
分析:(1)根据一组对边平行且相等的四边形是平行四边形判断出四边形BFCE是平行四边形,根据平行四边形的对边平行可得BF∥CE,对边相等可得BF=CE,从而得到AB=BF,再根据两直线平行,同旁内角互补求出∠DBF=90°,然后利用“边角边”证明△ABE和△BFD全等,根据全等三角形对应边相等可得DF=BE,全等三角形对应角相等可得∠ABE=∠BFD,再求出∠CFD=90°,从而判断出△CDF是等腰直角三角形,根据等腰直角三角形的性质可得DC=
CF,然后相比即可得解;
(2)过点C作CF∥BE且是CF=BE,判断出四边形BFCE是平行四边形,根据平行四边形的对边互相平行可得BF∥CE,然后根据两直线平行,同旁内角互补求出∠DBF=90°,再根据两边对应成比例,夹角相等,两三角形相似求出△ABE和△BFD相似,根据相似三角形对应边成比例可得
=
=k,相似三角形对应角相等可得∠ABE=∠BFD,然后求出∠DCF=90°,利用勾股定理列式用CF表示出DC,然后列出方程求解即可.
| 2 |
(2)过点C作CF∥BE且是CF=BE,判断出四边形BFCE是平行四边形,根据平行四边形的对边互相平行可得BF∥CE,然后根据两直线平行,同旁内角互补求出∠DBF=90°,再根据两边对应成比例,夹角相等,两三角形相似求出△ABE和△BFD相似,根据相似三角形对应边成比例可得
| DF |
| BE |
| BD |
| AE |
解答:解:(1)∵CF∥EB,且CF=EB,
∴四边形BFCE是平行四边形,
∴BF∥CE,BF=CE,
∴∠DBF=180°-∠A=180°-90°=90°,
∵∠A=90°,
∴∠A=∠DBF,
∵CE=AB,
∴AB=BF,
在△ABE和△BFD中,
,
∴△ABE≌△BFD(SAS),
∴DF=BE,∠ABE=∠BFD,
∵CF∥BE,
∴∠EBF+∠BFC=180°,
∴∠CFD=180°-∠BFD-∠EBF=180°-∠ABE-∠EBF=180°-∠ABF=180°-90°=90°,
∴△CDF是等腰直角三角形,
∴DC=
CF,
∵CF=EB,
∴
=
;
(2)如图,过点C作CF∥BE且是CF=BE,
则四边形BFCE是平行四边形,
∴BF∥CE,BF=CE,
∴∠DBF=180°-∠A=180°-90°=90°,
∵∠A=90°,
∴∠A=∠DBF,
∵CE=kAB,BD=kAE,
∴
=
=k,
∴△ABE∽△BFD,
∴
=
=k,∠ABE=∠BFD,
∵CF=BE,
∴
=
=k,
∴DF=kCF,
∵CF∥BE,
∴∠EBF+∠BFC=180°,
∴∠CFD=180°-∠BFD-∠EBF=180°-∠ABE-∠EBF=180°-∠ABF=180°-90°=90°,
由勾股定理得,DC=
=
=
CF,
∴
=
,
∵
=
,EB=CF,
∴
=
,
两边平方并整理得,k2=3,
解得k=
,k=-
(舍去).
∴四边形BFCE是平行四边形,
∴BF∥CE,BF=CE,
∴∠DBF=180°-∠A=180°-90°=90°,
∵∠A=90°,
∴∠A=∠DBF,
∵CE=AB,
∴AB=BF,
在△ABE和△BFD中,
|
∴△ABE≌△BFD(SAS),
∴DF=BE,∠ABE=∠BFD,
∵CF∥BE,
∴∠EBF+∠BFC=180°,
∴∠CFD=180°-∠BFD-∠EBF=180°-∠ABE-∠EBF=180°-∠ABF=180°-90°=90°,
∴△CDF是等腰直角三角形,
∴DC=
| 2 |
∵CF=EB,
∴
| EB |
| DC |
| ||
| 2 |
(2)如图,过点C作CF∥BE且是CF=BE,
则四边形BFCE是平行四边形,

∴BF∥CE,BF=CE,
∴∠DBF=180°-∠A=180°-90°=90°,
∵∠A=90°,
∴∠A=∠DBF,
∵CE=kAB,BD=kAE,
∴
| BF |
| AB |
| BD |
| AE |
∴△ABE∽△BFD,
∴
| DF |
| BE |
| BD |
| AE |
∵CF=BE,
∴
| DF |
| CF |
| DF |
| BE |
∴DF=kCF,
∵CF∥BE,
∴∠EBF+∠BFC=180°,
∴∠CFD=180°-∠BFD-∠EBF=180°-∠ABE-∠EBF=180°-∠ABF=180°-90°=90°,
由勾股定理得,DC=
| DF2+CF2 |
| (kCF)2+CF2 |
| k2+1 |
∴
| CF |
| DC |
| 1 | ||
|
∵
| EB |
| DC |
| 1 |
| 2 |
∴
| 1 | ||
|
| 1 |
| 2 |
两边平方并整理得,k2=3,
解得k=
| 3 |
| 3 |
点评:本题是相似形综合题,主要利用了平行四边形的判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,(1)求出△CDF是等腰直角三角形是解题的关键,难点在于(2)利用(1)的思路作辅助线构造出相似三角形以及直角三角形.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
下列方程中,解为x=2的方程是( )
| A、4x=2 | ||
| B、7x-14=0 | ||
C、
| ||
| D、3x+6=0 |
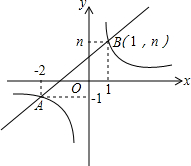 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=