题目内容
1.我们给出如下新定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.(1)如图①,请你在图中画出以格点为顶点,OA、OB为勾股边且对角线相等的勾股四边形OAPB;
(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连结AD、DC.若∠DCB=30°.则四边形ABCD是勾股四边形,为什么?
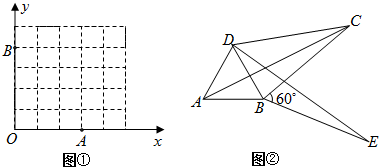
分析 (1)OM=AB知以格点为顶点的M共两个:M(3,4)或M(4,3).
(2)需要证明DC2+BC2=AC2,只需证明∠DCE=90°.
解答 (1)解:答案如图所示.M(3,4)或M′(4,3).
(2)证明:连接EC,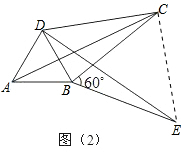
∵△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60°,
∴EC=BC=BE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
即四边形ABCD是勾股四边形.
点评 本题考查勾股定理,及考查旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
12.某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需化简):
(2)如果销售这批T恤获得的利润用W元表示,求W与x之间的函数关系式;
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
(1)填表(不需化简):
| 时 间 | 第一个月 | 第二个月 | 清仓时 |
| 单 价(元) | 80 | 40 | |
| 销售量(件) | 200 |
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
9.下列计算中,正确的是( )
| A. | 2a2+3a2=5a2 | B. | (a-b)2=a2-b2 | C. | a3•a2=a6 | D. | (-2a3)2=8a6 |
16.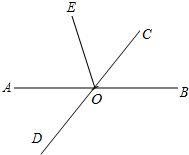 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |