题目内容
证明:已知两个三角形三条中线对应相等,那么这两个三角形全等.
考点:全等三角形的判定
专题:证明题
分析:分别过C,C'两点分别作AD和A′D′的平行线,分别交于BE和B′E′的延长线于G,G′点,利用重心的性质可证明△OGC≌△O'G'C',进一步可证明△OEC≌△O′E′C′,可得出AC=A′C′,同理可证明BC=B′C′,AB=A′B′,可证得△ABC≌△A′B′C′.
解答: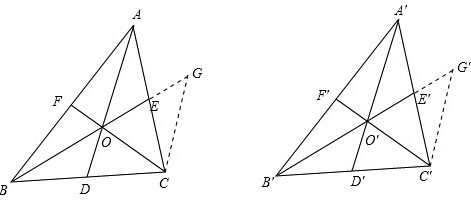 已知:在△ABC和△A′B′C′中,AD,BE,CF分别是△ABC的三条中线,相交于点O,A′D′,B′E′,C′F′分别是△A′B′C′的三条中线,相交于点O′,且AD=A′D′,BE=B′E′,CF=C′F′,
已知:在△ABC和△A′B′C′中,AD,BE,CF分别是△ABC的三条中线,相交于点O,A′D′,B′E′,C′F′分别是△A′B′C′的三条中线,相交于点O′,且AD=A′D′,BE=B′E′,CF=C′F′,
求证:△ABC≌△A′B′C′,
证明:分别过C,C'两点分别作AD和A′D′的平行线,分别交于BE和B′E′的延长线于G,G′点,
则AO=CG,A′O'=C′G′,BO=OG,B′O′=O′G′,
由已知条件AD=A′D′,BE=B′E′,CF=C′F′,
可得GC=G′C′,OG=O′G′,OC=O′C′
在△OGC和△O′G′C′中
∴△OGC≌△O'G'C'(SSS),
∴∠EOC=∠E′O′C′
在△OEC和△O′E′C′中,
∴△OEC≌△O′E′C′(SAS),
∴CE=C′E′,
∴AC=A′C′,
同理可证明AB=A′B′,B′C′,
在△ABC和△A′B′C′中
∴△ABC≌△A'B'C'(SSS).
 已知:在△ABC和△A′B′C′中,AD,BE,CF分别是△ABC的三条中线,相交于点O,A′D′,B′E′,C′F′分别是△A′B′C′的三条中线,相交于点O′,且AD=A′D′,BE=B′E′,CF=C′F′,
已知:在△ABC和△A′B′C′中,AD,BE,CF分别是△ABC的三条中线,相交于点O,A′D′,B′E′,C′F′分别是△A′B′C′的三条中线,相交于点O′,且AD=A′D′,BE=B′E′,CF=C′F′,求证:△ABC≌△A′B′C′,
证明:分别过C,C'两点分别作AD和A′D′的平行线,分别交于BE和B′E′的延长线于G,G′点,
则AO=CG,A′O'=C′G′,BO=OG,B′O′=O′G′,
由已知条件AD=A′D′,BE=B′E′,CF=C′F′,
可得GC=G′C′,OG=O′G′,OC=O′C′
在△OGC和△O′G′C′中
|
∴△OGC≌△O'G'C'(SSS),
∴∠EOC=∠E′O′C′
在△OEC和△O′E′C′中,
|
∴△OEC≌△O′E′C′(SAS),
∴CE=C′E′,
∴AC=A′C′,
同理可证明AB=A′B′,B′C′,
在△ABC和△A′B′C′中
|
∴△ABC≌△A'B'C'(SSS).
点评:本题主要考查全等三角形的判定和性质,利用条件构造三角形全等,证明出AC=A′C′是解题的关键,解题中注意重心的性质的利用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
月球的质量约为73400 000 000亿吨,用科学记数法表示这个数是( )
| A、734×108亿吨 |
| B、73.4×109亿吨 |
| C、7.34×1010亿吨 |
| D、0.734×1011亿吨 |
 如图,△ABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,△DBC的周长是25cm,则BC=
如图,△ABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,△DBC的周长是25cm,则BC= 如图,∠1的同位角是
如图,∠1的同位角是