题目内容
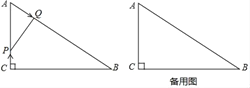
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
【答案】1+ ![]()
【解析】解:设正方形OABC的边长为m,和正方形CDEF的边长为n.
∵点M为OC的中点,
∴点M为(0, ![]() )、点B为(m,m)和点E为(n,m+n),
)、点B为(m,m)和点E为(n,m+n),
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+ ![]() ,
,
解得:a= ![]() ,
,
∴抛物线y= ![]() x2+
x2+ ![]() ,
,
把点E(n,m+n)代入抛物线得
m+n= ![]() n2+
n2+ ![]() ,
,
解得:n=m+ ![]() m或n=m﹣
m或n=m﹣ ![]() m(不合题意,舍去),
m(不合题意,舍去),
即CB=m,EF=m+ ![]() m,
m,
∴ ![]() =1+
=1+ ![]() .
.
设正方形OABC的边长为m,和正方形CDEF的边长为n.又点M为OC的中点,从而得出M,B,E三点的坐标,根据待定系数法求出抛物线的解析式,再把E点的坐标代入就可以得出用含m的式子表示n,从而表示出CB.EF的长度,进而得到其比值。

练习册系列答案
相关题目
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁