Question

如图①，点A是直线y=kx（k＞0，且k为常数）上一动点，以A为顶点的抛物线y=（x-h）²+m交直线y=kx于另一点E，交y轴于点F，抛物线的对称轴交x轴于点B，交直线EF于点C（点A、E、F两两不重合）．
（Ⅰ）写出h与m之间的关系（用含k的代数式表示）；
（Ⅱ）当点A运动到使EF与x轴平行时（如图②），求

AC

OF

的值；
（Ⅲ）当点A运动到使点F的位置最低时（如图③），求

AC

OF

的值．

Answer 1

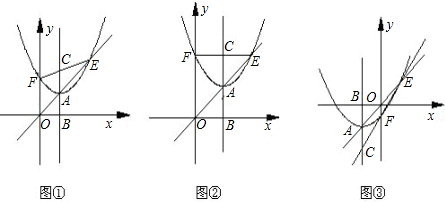
分析：（Ⅰ）由于抛物线的顶点（h，m）在直线y=kx上，把顶点坐标代入解析式中即可得到h与m之间的关系；
（Ⅱ）当EF与x轴平行时，点E与点F关于抛物线的对称轴对称，根据轴对称的性质得到FC=CE，然后利用CA∥y轴怎么△ECA∽△EFO，最后利用相似三角形的性质即可得到

AC

OF

的值；
（Ⅲ）当点F的位置处于最低时，其纵坐标h²+kh最小，而h2+kh=[h2+kh+(

1

2

k)2]-

1

4

k2=(h+

1

2

k)2-

1

4

k2，当h=-

1

2

k时，点F的位置最低，此时F（0，-

1

4

k2），然后解方程组

y=(x+ 1 2 k)2- 1 2 k2 y=kx.

得E的坐标（

1

2

k，

1

2

k2），同时确定A的坐标（-

1

2

k，-

1

2

k2），然后利用待定系数法可以确定直线EF的解析式，最后把x=-

1

2

k代入直线EF的解析式中确定即点C的坐标，最后分别可以求出线段AC的长度，OF的长度解决问题．

解答：解：（Ⅰ）∵抛物线的顶点（h，m）在直线y=kx上，
∴m=kh；

（Ⅱ）当EF与x轴平行时，点E与点F关于抛物线的对称轴对称，
∴FC=CE．
∵CA∥y轴，
∴△ECA∽△EFO．
∴

AC

OF

=

EC

EF

=

1

2

；

（Ⅲ）当点F的位置处于最低时，其纵坐标h²+kh最小，（5分）
∵h2+kh=[h2+kh+(

1

2

k)2]-

1

4

k2=(h+

1

2

k)2-

1

4

k2，
当h=-

1

2

k时，点F的位置最低，此时F（0，-

1

4

k2）．（6分）
解方程组

y=(x+ 1 2 k)2- 1 2 k2 y=kx.

，
得E（

1

2

k，

1

2

k2），A（-

1

2

k，-

1

2

k2）．（7分）
设直线EF的解析式为y=px+q，
将点E（

1

2

k，

1

2

k2），F（0，-

1

4

k2）的横纵坐标分别代入，
得

1 2 k2= 1 2 kp+q - 1 4 k2=q

．（8分）
解得

p= 3 2 k q=- 1 4 k2.

∴直线EF的解析式为y=

3

2

kx-

1

4

k2．（9分）
当x=-

1

2

k时，y=-k²，
即点C的坐标为（-

1

2

k，-k²），
∵点A（-

1

2

k，-

1

2

k2），
∴AC=

1

2

k2，
而OF=

1

4

k2，
∴

AC

OF

=

1 2 k2

1 4 k2

=2．（10分）

点评：本题考查的是二次函数的综合题型，其中涉及的知识点有抛物线的平移、函数图象的交点坐标与其解析式的组成的方程组的解的关系及相似三角形的性质与判定，综合性比较强，对学生的能力要求比较高，平时加强训练．