题目内容
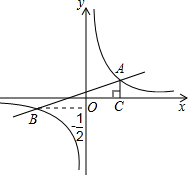 如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.求:
,过点A作AC⊥x轴于点C,AC=1,OC=2.求:
(1)求反比例函数的解析式和一次函数的解析式;
(2)求不等式kx+b- <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
解:(1)∵AC=1,OC=2,
∴A点坐标为:(2,1),
将A点坐标代入y2= ,
,
解得;m=2,
则y2= ;
;
∵点B的纵坐标为 ,
,
∴点B的横坐标为:- =
= ,
,
解得:x=-4,
故B点坐标为:(-4,- ),
),
将A,B两点坐标代入y1=kx+b得:
 ,
,
解得:
y1= x+
x+ ;
;
(2)∵不等式kx+b- <0的解集即为:y1<y2的解集,
<0的解集即为:y1<y2的解集,
∴-4<x<0或x>2.
分析:(1)由题意得,AC=1,OC=2,得出A点坐标,再将点A代入即可得出m,将AB两点代入一次函数y=kx+b求出k、b,从而得出答案;
(2)一次函数在反比例函数图象的上方时,自变量x的取值范围即可.
点评:本题考查了反比例函数和一次函数的交点问题,熟练掌握函数解析式的求法以及利用数形结合得出函数值大小关系是重点.
∴A点坐标为:(2,1),
将A点坐标代入y2=
 ,
,解得;m=2,
则y2=
 ;
;∵点B的纵坐标为
 ,
,∴点B的横坐标为:-
 =
= ,
,解得:x=-4,
故B点坐标为:(-4,-
 ),
),将A,B两点坐标代入y1=kx+b得:
 ,
,解得:

y1=
 x+
x+ ;
; (2)∵不等式kx+b-
 <0的解集即为:y1<y2的解集,
<0的解集即为:y1<y2的解集,∴-4<x<0或x>2.
分析:(1)由题意得,AC=1,OC=2,得出A点坐标,再将点A代入即可得出m,将AB两点代入一次函数y=kx+b求出k、b,从而得出答案;
(2)一次函数在反比例函数图象的上方时,自变量x的取值范围即可.
点评:本题考查了反比例函数和一次函数的交点问题,熟练掌握函数解析式的求法以及利用数形结合得出函数值大小关系是重点.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
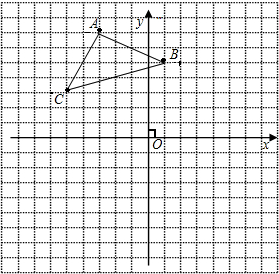 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),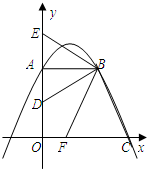 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
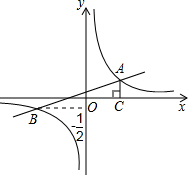 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示