Question

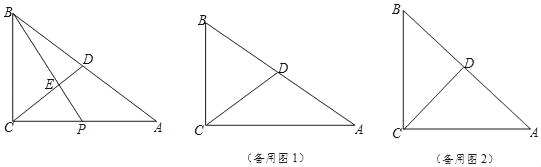
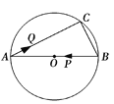
【题目】如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°．若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t（s），当△APQ是直角三角形时，t的值为 ．

Answer 1

【答案】或3-

【解析】

试题因为AB是⊙O的直径，所以∠ACB=90°，又因为BC=2，∠ABC=60°；所以AB=2BC=4cm；因为运动时间为t（s），所以AQ=t，BP=2t，所以AP=4-2t，

①当∠AQP=90°时， 因为∠A=30°，AP=4-2t，所以PQ=2-t，AQ= PQ，所以t= （2-t），所以t=3-；②当∠APQ=90°时，PQ=AQ，AP=PQ，所以4-2t=，解得t=，

综上所述，当t的值为或3-时，△APQ是直角三角形．