Question

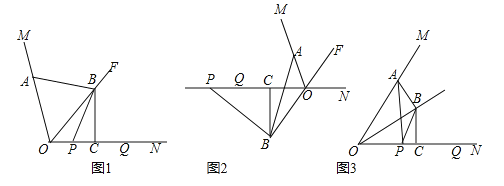
【题目】 （1）问题感知 如图1，在△ABC中，∠C＝90°，且AC＝BC，点P是边AC的中点，连接BP，将线段PB绕点P顺时针旋转90°到线段PD．连接AD．过点P作PE∥AB交BC于点E，则图中与△BEP全等的三角形是　 　，∠BAD＝　 　°；

（2）问题拓展 如图2，在△ABC中，AC＝BC＝AB，点P是CA延长线上一点，连接BP，将线段PB绕点P顺时针旋转到线段PD，使得∠BPD＝∠C，连接AD，则线段CP与AD之间存在的数量关系为CP＝AD，请给予证明；

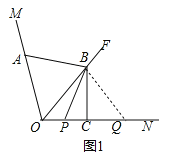
（3）问题解决 如图3，在△ABC中，AC＝BC＝AB＝2，点P在直线AC上，且∠APB＝30°，将线段PB绕点P顺时针旋转60°到线段PD，连接AD，请直接写出△ADP的周长．

Answer 1

【答案】（1）△PAD，90；（2）证明见解析；（3）．

【解析】

（1）由“SAS”可证△PAD≌△BEP，可得∠PAD=∠BEP=135°，依据∠ABC=45°，可得∠BAD=90°；
（2）过点P作PH∥AB，交CB的延长线于点H，由“SAS”可证△APD≌△HBP，可得PH=AD，通过证明△CAB∽△CPH，可得，即可得结论；
（3）分两种情况讨论，由直角三角形的性质和相似三角形的性质可求解．

证明：（1）∵点P是边AC的中点，PE∥AB，

∴点E是BC的中点，

∴CE＝BE，

∵AC＝BC，

∴BE＝AP，

∵将线段PB绕点P顺时针旋转90°到线段PD．

∴PB＝PD，

∵∠APD+∠BPC＝90°，∠EBP +∠BPC＝90°，

∴∠EBP＝∠APD，

又∵PB＝PD，

∴△PAD≌△BEP（SAS），

∴∠PAD＝∠BEP，

∵∠C＝90°，AC＝BC，

∴∠BAC＝∠ABC＝45°，

∵PE∥AB，

∴∠ABC＝∠PEC＝45°，

∴∠BEP＝135°，

∴∠BAD＝∠PAD﹣∠BAC＝135°﹣45°＝90°，

故答案为：△PAD，90；

（2）如图，过点P作PH∥AB，交CB的延长线于点H，

∴∠CBA＝∠CHP，∠CAB＝∠CPH，

∵CB＝CA，

∴∠CBA＝∠CAB，

∴∠CHP＝∠CPH，

∴CH＝CP，

∴BH＝AP，

∵将线段PB绕点P顺时针旋转90°到线段PD．

∴PB＝PD，

∵∠BPD＝∠C，

∴∠BPD+∠BPC＝∠C+∠BPC，

∴∠PBH＝∠APD，

∴△APD≌△HBP（SAS），

∴PH＝AD，

∵PH∥AB，

∴△CAB∽△CPH，

∴

∴

∵AC＝BC＝AB，

∴，

∴CP＝PH＝AD；

（3）当点P在CA的延长线上时，

∵AC＝BC＝AB＝2，

∴△ABC是等边三角形，

∴∠ACB＝60°，

∵将线段PB绕点P顺时针旋转60°到线段PD，

∴BP＝PD，∠BPD＝60°＝∠ACB，

过点P作PE∥AB，交CB的延长线于点E，

∵∠ACB＝∠APB+∠ABP，

∴∠ABP＝∠APB＝30°，

∴AB＝AP＝2，

∴CP＝4，

∵AB∥PE，

∴

∴CP＝PE＝4，

由（2）得，PE＝AD＝4，

∵∠APD＝∠APB+BPD＝90°，

∴DP＝，

∴△ADP的周长＝AD+AP+DP＝+6，

当点P在AC延长线上时，如图，

同理可求△ADP的周长＝6+，

综上所述：△ADP的周长为6+．