题目内容
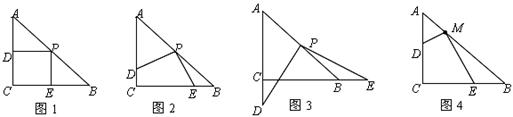
已知:如图所示, 为任意三角形,若将
为任意三角形,若将 绕点
绕点 顺时针旋转180° 得到
顺时针旋转180° 得到 .
.

(1)试猜想 与
与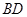 有何关系?说明理由;
有何关系?说明理由;
(2)请给 添加一个条件,使旋转得到的四边形
添加一个条件,使旋转得到的四边形 为矩形,并说明理由.
为矩形,并说明理由.
 为任意三角形,若将
为任意三角形,若将 绕点
绕点 顺时针旋转180° 得到
顺时针旋转180° 得到 .
.
(1)试猜想
 与
与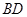 有何关系?说明理由;
有何关系?说明理由;(2)请给
 添加一个条件,使旋转得到的四边形
添加一个条件,使旋转得到的四边形 为矩形,并说明理由.
为矩形,并说明理由.(1)AE∥BD,AE=BD;(2)AC=BC
试题分析:(1)根据旋转的性质可得
 ≌
≌ ,即得AB=DE,∠ABC=∠DEC,则可得到四边形ABDE为平行四边形,从而可以得到结论;
,即得AB=DE,∠ABC=∠DEC,则可得到四边形ABDE为平行四边形,从而可以得到结论;(2)根据旋转的性质,可得AC=BC=CE=CD,再结合AC=BC即可作出判断.
(1)AE∥BD,AE=BD
理由:∵
 绕点C顺时针旋转180°得到
绕点C顺时针旋转180°得到 ,
,∴
 ≌
≌ ,
,∴AB=DE,∠ABC=∠DEC,
∴AB∥DE,
∴四边形ABDE为平行四边形,
∴AE∥BD,AE=BD;
(2)AC="BC"
∵AC=BC,根据旋转的性质,可得AC=BC=CE=CD,
∴AD=BE,
∴四边形ABDE是矩形.
点评:特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



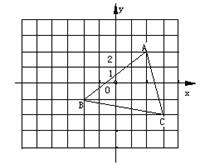
 OABC的两个顶点A、C的坐标分别为(1,2)、(3,0).
OABC的两个顶点A、C的坐标分别为(1,2)、(3,0).