Question

已知反比例函数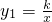和二次函数y₂=-x²+bx+c的图象都过点A（-1，2）
（1）求k的值及b、c的数量关系式（用c的代数式表示b）；
（2）若两函数的图象除公共点A外，另外还有两个公共点B（m，1）、C（1，n），试在如图所示的直角坐标系中画出这两个函数的图象，并利用图象回答，x为何值时，y₁＜y₂；
（3）当c值满足什么条件时，函数y₂=-x²+bx+c在x≤-的范围内随x的增大而增大？

Answer 1

解：（1）将A（-1，2）代入反比例函数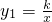中，
可得k=（-1）×2=-2，
将A（-1，2）代入二次函数y₂=-x²+bx+c
可得2=-1-b+c，
即b=c-3．

（2）由题意可知，B的坐标为（-2，1），C的坐标为（1，-2）．
反比例函数的解析式为y₁=-，
抛物线的解析式为y₂=-x²-2x+1．

（3）如图：
由图可知：当-2＜x＜-1和0＜x＜1时，y₁＜y₂．
即-≤-，-≤-，
解得c≤2．
分析：（1）将点A的坐标代入两函数的解析式中即可得出k的值，以及b与c的数量关系．
（2）在（1）中已得出了反比例函数的解析式，那么可根据B，C两点都在反比例函数上可求出B，C的坐标，然后根据B，C的坐标用待定系数法求出抛物线的解析式．进而可根据两函数的解析式来得出函数的图形，以及y₁＜y₂时，x的取值范围．
（3）由于抛物线开口向下，因此对称轴左边，抛物线上的点都是随x的增大而增大，那么对称轴-≤-，然后再根据（1）中b，c的大小关系即可求出c的取值范围．
点评：本题主要考查了反比例函数和二次函数的综合知识，利用条件来确定b，c的值或数量关系是解题的关键．