题目内容
已知函数 (
( 是常数)
是常数)
(1)若该函数的图像与 轴只有一个交点,求
轴只有一个交点,求 的值;
的值;
(2)若点 在某反比例函数的图像上,要使该反比例函数和二次函数
在某反比例函数的图像上,要使该反比例函数和二次函数 都是
都是 随
随 的增大而增大,求
的增大而增大,求 应满足的条件以及
应满足的条件以及 的取值范围;
的取值范围;
(3)设抛物线 与
与 轴交于
轴交于 两点,且
两点,且 ,
, ,在
,在 轴上,是否存在点P,使△ABP是直角三角形?若存在,求出点P及△ABP的面积;若不存在,请说明理由。
轴上,是否存在点P,使△ABP是直角三角形?若存在,求出点P及△ABP的面积;若不存在,请说明理由。
【答案】
解:(1)①当 时,函数为
时,函数为 为一次函数,它的图像与x轴只有一个交点。
为一次函数,它的图像与x轴只有一个交点。
②当 时,若函数
时,若函数 的图像与x轴只有一个交点,则方程
的图像与x轴只有一个交点,则方程 有两个相等的实数根,所以
有两个相等的实数根,所以 ,解得
,解得 。
。
综上所述,若函数的图像与x轴只有一个交点,则 的值为0或
的值为0或 。
。
(2)设反比例函数为 ,
,
∵点 在反比例函数的图像上,∴
在反比例函数的图像上,∴ ,即
,即 .。
.。
∴反比例函数为 。
。
∵要使该反比例函数y随着x的增大而增大,则 。
。
∵二次函数 的对称轴为
的对称轴为 ,
,
∴要使二次函数 的y随着x的增大而增大,在
的y随着x的增大而增大,在 的情况下,x必须在对称轴的左边,即
的情况下,x必须在对称轴的左边,即 。
。
综上所述,要使该反比例函数和二次函数都y随着x的增大而增大,必须 且
且 。
。
(3)存在。
∵抛物线 与x轴有两个交点,
与x轴有两个交点,
∴一元二次方程方程 的判别式
的判别式 ,解得
,解得 。
。
又∵ ,∴
,∴ ,解得
,解得 或
或 。
。
又∵ ,∴
,∴ 。
。
∴二次函数为 。
。
设P(0,p)是满足条件的点,则 ,即
,即 。
。
∴ 。∴
。∴ 。∴
。∴ 。
。
∴ 。∴
。∴ 。
。
∴ 。
。
∴在y轴上,存在点P(0, )或(0,
)或(0, ),使△ABP是直角三角形,△ABP的面积为
),使△ABP是直角三角形,△ABP的面积为 。
。
【解析】(1)分 和
和 两种情况讨论即可。
两种情况讨论即可。
(2)根据二次函数和反比例函数的性质求解。
(3)若△ABP是直角三角形,则一定是∠APB=900,从而由已知 ,
, ,根据一元二次方程根的判别式和根与系数的关系,求出k的值,进而根据勾股定理即可求得点P的坐标,求得△ABP的面积。
,根据一元二次方程根的判别式和根与系数的关系,求出k的值,进而根据勾股定理即可求得点P的坐标,求得△ABP的面积。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 为何值,该函数的图象都经过
为何值,该函数的图象都经过 轴上的一个定点;
轴上的一个定点;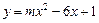 (
(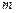 是常数).
是常数).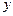 轴上的一个定点;
轴上的一个定点;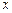 轴只有一个交点,求
轴只有一个交点,求 (
(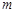 是常数).
是常数). 轴上的一个定点;
轴上的一个定点;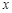 轴只有一个交点,求
轴只有一个交点,求