题目内容
4.对于函数y=x+$\frac{a}{x}$(a>0,x>0),当x=$\frac{a}{x}$,即x=$\sqrt{a}$时,函数y有最小值,最小值为2$\sqrt{a}$,即y=x+$\frac{a}{x}$≥$2\sqrt{x•\frac{a}{x}}=2\sqrt{a}$.根据上述结论,回答下列问题:
(1)对于函数y1=x(x>0)与函数y2=$\frac{1}{x}$(x>0),当x=1时,y1+y2取得最小值,最小值为2.
(2)对于函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),$\frac{{y}_{2}}{{y}_{1}}$的最小值是4.
(3)已知某汽车的一次运输成本包含以下三个部分:一是固定费用360元;二是燃油费,每千米为1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001,设该汽车某次云舒的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低运输成本是多少?
分析 (1)根据题目中所给的方法解答即可;
(2)把(x+1)看作一个整体求解即可;
(3)根据运输成本的组成列式表示出汽车平均每千米的运输成本,然后根据题目中所给的方法解答即可.
解答 解:
(1)y1+y2=x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当x=$\frac{1}{x}$,即x=1时取等号,
∴当x=1时,y1+y2取得最小值为2;
故答案为:1;2;
(2)∵$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+4}{x+1}$=(x+1)+$\frac{4}{x+1}$≥2$\sqrt{(x+1)×\frac{4}{x+1}}$=4,
当x+1=$\frac{4}{x+1}$,即x=1时,取等号,
∴当x=1时,$\frac{{y}_{2}}{{y}_{1}}$的最小值为4,
故答案为:4;
(3)汽车平均每千米的运输成本=$\frac{360+1.6x+0.001{x}^{2}}{x}$=$\frac{360}{x}$+0.001x+1.6,
∵$\frac{360}{x}$+0.001x≥2$\sqrt{\frac{360}{x}×0.001x}$=1.2,
∴汽车平均每千米的运输成本最低是1.2+1.6=2.8元,
当$\frac{360}{x}$=0.001x,即x=600千米时,取等号,
答:当x为600千米时,该汽车平均每千米的运输成本最低为2.8元.
点评 本题为反比例函数的综合应用,读懂题目信息,理解题目中的最小值的求法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.不透明的布袋中有2个红球和3个白球,所有球除颜色外无其它差别,某同学从布袋里任意摸出一个球,则他摸出红球的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
19.某果园2015年水果产量为a吨,2016年因干旱影响产量下降15%,2017年新增滴灌系统,预计产量能在2016年基础上上升20%,估计2017年该果园水果产量为( )
| A. | (1-15%)(1+20%)a吨 | B. | (1-15%)20%a吨 | C. | (1+15%)(1-20%)a吨 | D. | (1+20%)15%a吨 |
9.在“国际禁烟日”当天,某学习小组为了了解某社区6000个成年人中大约有多少人吸烟,随机抽查了200个成年人,结果其中有10个成年人吸烟,对于这个数据收集和处理问题,下列说法正确的是( )
| A. | 调查的方式是普查 | B. | 样本容量是200 | ||
| C. | 该小区只有190个成年人不吸烟 | D. | 该小区一定有300人吸烟 |
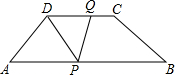 如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点P从A开始沿AB边向B以每秒3cm的速度移动,点Q从C开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时运动停止,设运动时间为t秒.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点P从A开始沿AB边向B以每秒3cm的速度移动,点Q从C开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时运动停止,设运动时间为t秒. 如图,已知:AB=AD,BC=CD,AE⊥BC,垂足为E,AF⊥CD,垂足为F.求证:
如图,已知:AB=AD,BC=CD,AE⊥BC,垂足为E,AF⊥CD,垂足为F.求证: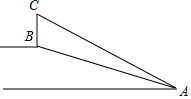 某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)
某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)