题目内容
一次函数y=kx+b,当-2≤x≤2时,对应的y值为1≤y≤9,则kb值为
- A.10
- B.-12
- C.-10或10
- D.-10或12
C
分析:因为函数的增减没有明确,所以分k>0时,y随x的增大而增大,k<0时,y随x的增大而减小两种情况,列方程组求出k、b的值,再求kb即可.
解答:(1)当k>0时,y随x的增大而增大,
∴ ,
,
解得 ,
,
∴kb=2×5=10;
(2)当k<时,y随x的增大而减小,
∴ ,
,
解得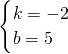 ,
,
∴kb=-2×5=-10.
因此kb的值为-10或10.
故选C.
点评:本题主要考查一次函数的性质,因为k的正负情况不明确,所以需要分两种情况讨论.
分析:因为函数的增减没有明确,所以分k>0时,y随x的增大而增大,k<0时,y随x的增大而减小两种情况,列方程组求出k、b的值,再求kb即可.
解答:(1)当k>0时,y随x的增大而增大,
∴
 ,
,解得
 ,
,∴kb=2×5=10;
(2)当k<时,y随x的增大而减小,
∴
 ,
,解得
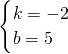 ,
,∴kb=-2×5=-10.
因此kb的值为-10或10.
故选C.
点评:本题主要考查一次函数的性质,因为k的正负情况不明确,所以需要分两种情况讨论.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
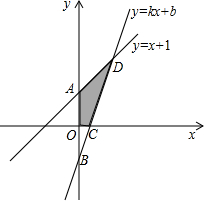 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D.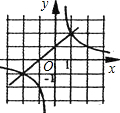 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y= (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,