题目内容
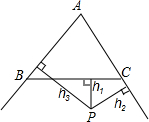 如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3-h1=6,那么等边△ABC的面积为( )
如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3-h1=6,那么等边△ABC的面积为( )A、12
| ||
B、9
| ||
C、8
| ||
D、4
|
分析:根据等边三角形的面积即可计算(h3+h2-h1)是等边三角形ABC的高,根据等边三角形的高即可求得BC的值,即可求得△ABC的面积,即可解题.
解答: 解:设等边△ABC的边长为a,连接PA、PB、PC,
解:设等边△ABC的边长为a,连接PA、PB、PC,
则S△PAB+S△PAC-S△PBC=S△ABC,
从而
ah3+
ah2-
ah1=
a2,
即
a(h3+h2-h1)=
a2,
∵(h3+h2-h1)=6,
∴a=4
,
∴S△ABC=
a2=12
.
故选A.
 解:设等边△ABC的边长为a,连接PA、PB、PC,
解:设等边△ABC的边长为a,连接PA、PB、PC,则S△PAB+S△PAC-S△PBC=S△ABC,
从而
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
即
| 1 |
| 2 |
| ||
| 4 |
∵(h3+h2-h1)=6,
∴a=4
| 3 |
∴S△ABC=
| ||
| 4 |
| 3 |
故选A.
点评:本题考查了等边三角形面积的计算,等边三角形高线长与边长的关系,本题中根据等边三角形的高计算等边三角形的面积是解题的关键.

练习册系列答案
相关题目
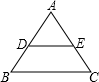
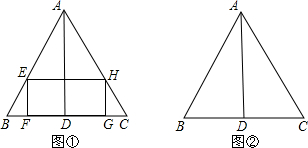
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动