题目内容
如图1,已知二次函数 的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
(1)求此二次函数的解析式和点C的坐标;
(2)当点D的坐标为(1,1)时,连接BD、BE.求证:BE平分∠ABD;
(3)点G在抛物线的对称轴上且位于第一象限,若以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,求点E的横坐标.

(1)解:∵点D(1,m)在 图象的对称轴上,
图象的对称轴上,
∴ .
.
∴b=-2.
∴二次函数的解析式为y=x2-2x-3=(x-1)2-4,
∴C(1,-4);
(2)证明:∵D(1,1),且DE垂直于y轴,
∴点E的纵坐标为1,DE平行于x轴.
∴∠DEB=∠EBO.
令y=1,则x2-2x-3=1,
解得: .
.
∵点E位于对称轴右侧,
∴E .
.
∴DE= .
.
令y=0,则x2-2x-3=0,求得点A的坐标为(3,0),点B的坐标为(-1,0).
∴BD= .
.
∴BD=DE.
∴∠DEB=∠DBE.
∴∠DBE=∠EBO.
∴BE平分∠ABD.
(3)解:∵以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,
且△GDE为直角三角形,
∴△ACG为直角三角形.
∵G在抛物线对称轴上且位于第一象限,
∴∠CAG=90°.
∵A(3,0)C(1,-4),AF⊥CG,
∴求得G点坐标为(1,1).
∴AG= ,AC=
,AC= .
.
∴AC=2AG.
∴GD=2DE或DE=2GD.
设E(t,t2-2t-3)(t>1),
①当点D在点G的上方时,则DE=t-1,
GD=(t2-2t-3)-1=t2-2t-4.
i.如图2,当GD=2DE时,
则有,t2-2t-4=2(t-1).
解得, .(舍负)
.(舍负)
ii.如图3,当DE=2GD时,
则有,t-1=2(t2-2t-4).
解得, .(舍负)
.(舍负)
②当点D在点G的下方时,则DE=t-1,
GD=1-(t2-2t-3)=-t2+2t+4.
i.如图4,当GD=2DE时,
则有,-t2+2t+4=2(t-1).
解得,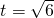 .(舍负)
.(舍负)
ii.如图5,当DE=2GD时,
则有,t-1=2(-t2+2t+4).
解得, .(舍负)
.(舍负)
综上,E点的横坐标为 或
或 或
或 或3.
或3.
分析:(1)利用点D(1,m)在此二次函数图象的对称轴上得出b的值,再利用配方法求出顶点坐标即可;
(2)首先得出E点坐标,进而得出BD=DE,即可得出BE平分∠ABD;
(3)利用①当点D在点G的上方时,②当点D在点G的下方时分别分类讨论得出即可.
点评:此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,利用分类讨论得出E点坐标是解题关键.
 图象的对称轴上,
图象的对称轴上,∴
 .
.∴b=-2.
∴二次函数的解析式为y=x2-2x-3=(x-1)2-4,
∴C(1,-4);
(2)证明:∵D(1,1),且DE垂直于y轴,
∴点E的纵坐标为1,DE平行于x轴.
∴∠DEB=∠EBO.
令y=1,则x2-2x-3=1,
解得:
 .
.∵点E位于对称轴右侧,
∴E
 .
.∴DE=
 .
.令y=0,则x2-2x-3=0,求得点A的坐标为(3,0),点B的坐标为(-1,0).
∴BD=
 .
.∴BD=DE.
∴∠DEB=∠DBE.
∴∠DBE=∠EBO.
∴BE平分∠ABD.
(3)解:∵以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,
且△GDE为直角三角形,
∴△ACG为直角三角形.
∵G在抛物线对称轴上且位于第一象限,

∴∠CAG=90°.
∵A(3,0)C(1,-4),AF⊥CG,
∴求得G点坐标为(1,1).
∴AG=
 ,AC=
,AC= .
.∴AC=2AG.
∴GD=2DE或DE=2GD.
设E(t,t2-2t-3)(t>1),
①当点D在点G的上方时,则DE=t-1,
GD=(t2-2t-3)-1=t2-2t-4.
i.如图2,当GD=2DE时,
则有,t2-2t-4=2(t-1).
解得,
 .(舍负)
.(舍负)
ii.如图3,当DE=2GD时,
则有,t-1=2(t2-2t-4).
解得,
 .(舍负)
.(舍负)②当点D在点G的下方时,则DE=t-1,
GD=1-(t2-2t-3)=-t2+2t+4.
i.如图4,当GD=2DE时,
则有,-t2+2t+4=2(t-1).
解得,
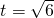 .(舍负)
.(舍负)ii.如图5,当DE=2GD时,
则有,t-1=2(-t2+2t+4).
解得,
 .(舍负)
.(舍负) 综上,E点的横坐标为
 或
或 或
或 或3.
或3.分析:(1)利用点D(1,m)在此二次函数图象的对称轴上得出b的值,再利用配方法求出顶点坐标即可;
(2)首先得出E点坐标,进而得出BD=DE,即可得出BE平分∠ABD;
(3)利用①当点D在点G的上方时,②当点D在点G的下方时分别分类讨论得出即可.
点评:此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,利用分类讨论得出E点坐标是解题关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 在平面直角坐标系xOy中(如图),已知二次函数y=x2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C.
在平面直角坐标系xOy中(如图),已知二次函数y=x2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C.

 (
( )的图象经过点
)的图象经过点 ,
, ,
, ,直线
,直线 (
( )与
)与 轴交于点
轴交于点 .
.
 (点
(点 为顶点的三角形与以
为顶点的三角形与以 为顶点的三角形相似,求
为顶点的三角形相似,求 的代数式表示);
的代数式表示); ,使得四边形
,使得四边形 为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.